Question

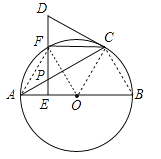
【题目】如图，AB是⊙O的直径，点P是弦AC上一动点（不与A，C重合），过点P作PE⊥AB，垂足为E，射线EP交于点F，交过点C的切线于点D．

（1）求证：DC=DP；

（2）若∠CAB=30°，当F是的中点时，判断以A，O，C，F为顶点的四边形是什么特殊四边形？说明理由．

Answer 1

【答案】（1）证明见解析；（2）以A，O，C，F为顶点的四边形是菱形．

【解析】

试题分析：（1）连接BC、OC，利用圆周角定理和切线的性质可得∠B=∠ACD，由PE⊥AB，易得∠APE=∠DPC=∠B，等量代换可得∠DPC=∠ACD，可证得结论；

（2）由∠CAB=30°易得△OBC为等边三角形，可得∠AOC=120°，由F是的中点，易得△AOF与△COF均为等边三角形，可得AF=AO=OC=CF，易得以A，O，C，F为顶点的四边形是菱形．

试题解析：（1）连接BC、OC，∵AB是⊙O的直径，∴∠OCD=90°，∴∠OCA+∠OCB=90°，∵∠OCA=∠OAC，∠B=∠OCB，∴∠OAC+∠B=90°，∵CD为切线，∴∠OCD=90°，∴∠OCA+∠ACD=90°，∴∠B=∠ACD，∵PE⊥AB，∴∠APE=∠DPC=∠B，∴∠DPC=∠ACD，∴AP=DC；

（2）以A，O，C，F为顶点的四边形是菱形．理由如下：

∵∠CAB=30°，∴∠B=60°，∴△OBC为等边三角形，∴∠AOC=120°，连接OF，AF，∵F是的中点，∴∠AOF=∠COF=60°，∴△AOF与△COF均为等边三角形，∴AF=AO=OC=CF，∴四边形OACF为菱形．