Question

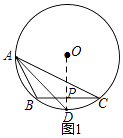
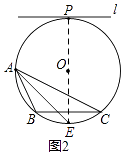
【题目】已知△ABC内接于⊙O，请仅用无刻度的直尺，根据下列条件分别在图1，图2中画出∠BAC的平分线（保留作图痕迹，不写作法）．
（1）如图1，P是BC边的中点；
（2）如图2，直线l与⊙O相切于点P，且l∥BC．

Answer 1

【答案】
（1）解：如图所示，AD 即为所求；

（2）解：如图所示，AE即为所求．

【解析】（1）连接OP并延长，交⊙O于D，根据P是BC边的中点，可得OD垂直平分BC，进而得到点D为 的中点，连接AD，则∠BAD=∠CAD，因此AD即为所求；（2）连接PO并延长，交⊙O于E，根据直线l与⊙O相切于点P，且l∥BC，可得PE垂直平分BC，进而得到点E为 的中点，连接AE，则∠BAE=∠CAE，因此AE即为所求．
【考点精析】解答此题的关键在于理解垂径定理的相关知识，掌握垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧，以及对圆周角定理的理解，了解顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半．