【题目】如图,△ABC中,∠C=90°,AD平分∠BAC,AD=4,CD=2,AC=2![]() ,则△ABD的面积是_______________.
,则△ABD的面积是_______________.

参考答案:
【答案】4![]()
【解析】
过点D作DE⊥AB于E,由直角三角形中一直角边等于斜边的一半,那么这条直角边所对的角等于30,得到∠CAD=30,从而∠B=30,再根据直角三角形中30角所对的直角边等于斜边的一半,得到AB=4![]() ,由AD平分∠BAC,可知DE,从而求得△ABD的面积.
,由AD平分∠BAC,可知DE,从而求得△ABD的面积.
解:过点D作DE⊥AB于E,
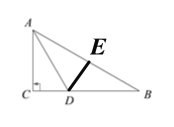
∵∠C=90,CD=2,AD=4,
∴∠CAD=30,
∵AD平分∠BAC,DE⊥AB,
∴∠CAB=60,CD=DE=2,
∴∠B=30,
∴AB=2AC=2×2![]() =4
=4![]() ,
,
∴S△ABD=![]() AB·DE=
AB·DE=![]() ×4
×4![]() ×2=4
×2=4![]() .
.
故答案为:4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点C,∠BGE=∠ADE.
(1)如图1,求证:AD=CD;
(2)如图2,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC 中,AB=AC=6cm,∠B=∠C,BC=4cm,点 D 为 AB的中点.
(1)如果点 P 在线段 BC 上以 1cm/s 的速度由点 B 向点 C 运动,同时,点 Q 在线段 CA 上由点 C 向点 A 运动.
①若点 Q 的运动速度与点 P 的运动速度相等,经过 1 秒后,△BPD 与△CQP 是否全等,请说明理由;
②若点 Q 的运动速度与点 P 的运动速度不相等,当点 Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?
(2)若点 Q 以②中的运动速度从点 C 出发,点 P 以原来的运动速度从点 B 同时出发,都逆时针沿△ABC 三边运动,则经过 后,点 P 与点 Q 第一次在△ABC 的 边上相遇?(在横线上直接写出答案,不必书写解题过程)

-
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
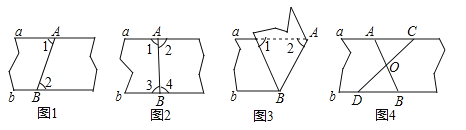
A. 如图1,展开后测得∠1=∠2
B. 如图2,展开后测得∠1=∠2且∠3=∠4
C. 如图3,测得∠1=∠2
D. 如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第 秒时,边CD恰好与边AB平行.

-
科目: 来源: 题型:
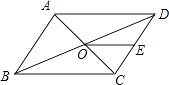
查看答案和解析>>【题目】如图,ABCD的周长为36,对角线AC,BD相交于点O.点E是CD的中点,BD=12,则△DOE的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(
 )﹣1﹣(π﹣3.14)0﹣
)﹣1﹣(π﹣3.14)0﹣ 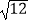 +2sin60°.
+2sin60°.
相关试题

