【题目】如图,已知直线![]() 的函数表达式为
的函数表达式为![]() ,它与
,它与![]() 轴、
轴、![]() 轴的交点分别为A、B两点.
轴的交点分别为A、B两点.
(1)求点A、B的坐标;
(2)设F是![]() 轴上一动点,⊙P经过点B且与
轴上一动点,⊙P经过点B且与![]() 轴相切于点F,设⊙P的圆心坐标为P(x,y),求y与
轴相切于点F,设⊙P的圆心坐标为P(x,y),求y与![]() 之间的函数关系;
之间的函数关系;
(3)是否存在这样的⊙P,既与![]() 轴相切,又与直线
轴相切,又与直线![]() 相切于点B?若存在,求出圆心P的坐标;若不存在,请说明理由.
相切于点B?若存在,求出圆心P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)A(﹣4,0),B(0,3); (2)y=![]() x2+
x2+![]() ; (3)存在.点
; (3)存在.点![]() 的坐标为(1,
的坐标为(1, ![]() )或(﹣9,15).
)或(﹣9,15).
【解析】试题分析:(1)根据坐标轴上点的坐标特征易得以A点坐标为(﹣4,0), B点坐标为(0,3),
(2)过点P作PD⊥y轴于D,则PD=![]() ,BD=
,BD=![]() ,根据切线的性质得PF=y,则PB=y,
,根据切线的性质得PF=y,则PB=y,
在Rt△BDP中,根据勾股定理得到y2=x2+(3﹣y)2 ,然后整理可得到:y=![]() x2+
x2+![]() ,
,
(3)因为⊙P与![]() 轴相切于点F,且与直线
轴相切于点F,且与直线![]() 相切于点B,根据切线长定理得到:AB=AF,而AB=5,所以AF=
相切于点B,根据切线长定理得到:AB=AF,而AB=5,所以AF=![]() 再把
再把![]() 分别代入y=
分别代入y=![]() x2+
x2+![]() 计算出对应的函数值,即可确定P点坐标.
计算出对应的函数值,即可确定P点坐标.
试题解析:(1)A点坐标为(﹣4,0),B点坐标为(0,3),
(2)过点P作PD⊥y轴于D,如图1,

则PD=|x|,BD=|3﹣y|,
∵⊙P经过点B且与x轴相切于点F,
∴PB=PF=y,
在Rt△BDP中,
∴PB2=PD2+BD2,
∴y2=x2+(3﹣y)2,
∴y=![]() x2+
x2+![]() ,
,
(3)存在.
如图2,∵⊙P与x轴相切于点F,且与直线l相切于点B,
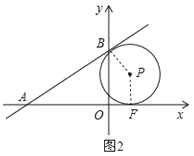
∴AB=AF,
∵AB2=OA2+OB2=52,
∴AF=5,
∵AF=|x+4|,
∴|x+4|=5,
∴x=1或x=﹣9,
当x=1时,y=![]() ,
,
当x=﹣9时,y=![]() =15,
=15,
∴点![]() 的坐标为(1,
的坐标为(1, ![]() )或(﹣9,15).
)或(﹣9,15).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a4+a5=a9B. a4a2=a8
C. a3÷a3=0D. (﹣a2 )3=﹣a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列语句:①画线段AB=CD;②互补的两个角是邻补角;③延长MN到点Q;④三角形的一边与另一边的延长线组成的角是三角形的外角吗?其中为命题的是_____.(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为建设美丽家园,某企业逐年增加对环境保护的经费投入,2012年投入了400万元,预计到2014年将投入576万元.
(1)求2012年至2014年该单位环保经费投入的年平均增长率;
(2)该单位预计2015年投入环保经费不低于680万元,若继续保持前两年的年平均增长率,该目标能否实现?请通过计算说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,相等关系一定成立的是( )
A. (x+6)(x﹣6)=x 2﹣6
B. (x﹣y)2=(y﹣x)2
C. (x﹣2)(x﹣6)=x 2﹣2x﹣6x﹣12
D. (x+y)2=x 2+y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.
(1)若生产第
 档次的产品一天的总利润为
档次的产品一天的总利润为 元(其中
元(其中 为正整数,且1≤
为正整数,且1≤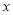 ≤10),求出
≤10),求出 关于
关于 的函数关系式;
的函数关系式;(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(m,n)在第二象限,那么点B(-m,│n│)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
相关试题

