Question

【题目】在平面直角坐标系中，已知抛物线（b，c为常数）的顶点为P，等腰直角三角形ABC的顶点A的坐标为（0，﹣1），C的坐标为（4，3），直角顶点B在第四象限．

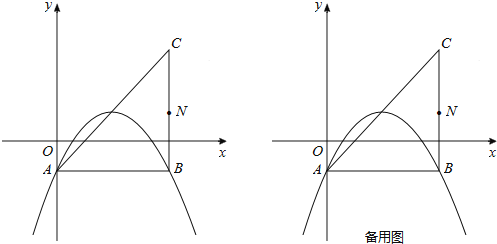
（1）如图，若该抛物线过A，B两点，求该抛物线的函数表达式；

（2）平移（1）中的抛物线，使顶点P在直线AC上滑动，且与AC交于另一点Q．

（i）若点M在直线AC下方，且为平移前（1）中的抛物线上的点，当以M、P、Q三点为顶点的三角形是等腰直角三角形时，求出所有符合条件的点M的坐标；

（ii）取BC的中点N，连接NP，BQ．试探究是否存在最大值？若存在，求出该最大值；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）（i）M1（4，﹣1），M2（﹣2，﹣7），M3（，），M4（，）；（ii）．

【解析】

试题分析：（1）先求出点B的坐标，然后利用待定系数法求出抛物线的函数表达式；

（2）（i）首先求出直线AC的解析式和线段PQ的长度，作为后续计算的基础．

若△MPQ为等腰直角三角形，则可分为以下两种情况：

①当PQ为直角边时：点M到PQ的距离为．此时，将直线AC向右平移4个单位后所得直线（y=x﹣5）与抛物线的交点，即为所求之M点；

②当PQ为斜边时：点M到PQ的距离为．此时，将直线AC向右平移2个单位后所得直线（y=x﹣3）与抛物线的交点，即为所求之M点．

（ii）由（i）可知，PQ=为定值，因此当NP+BQ取最小值时，有最大值．

如答图2所示，作点B关于直线AC的对称点B′，由分析可知，当B′、Q、F（AB中点）三点共线时，NP+BQ最小，最小值为线段B′F的长度．

试题解析：（1）∵等腰直角三角形ABC的顶点A的坐标为（0，﹣1），C的坐标为（4，3）

∴点B的坐标为（4，﹣1）．

∵抛物线过A（0，﹣1），B（4，﹣1）两点，∴，解得：b=2，c=﹣1，∴抛物线的函数表达式为：．

（2）（i）

∵A（0，1），C（4，3），∴lAC：y=x﹣1，∵抛物线顶点P在直线AC上，设P（t，t﹣1），∴抛物线表达式：，∴lAC与抛物线的交点Q（t﹣2，t﹣3），∵一M、P、Q三点为顶点的三角形是等腰直角三角形，P（t，t﹣1）：

①当M为直角顶点时，M（t，t﹣3），，∴t=，∴M1（，），M2（，）；

②当Q为直角顶点时，点M可视为点P绕点Q顺时针旋转90°而成，将点Q（t﹣2，t﹣3）平移至原点Q′（0，0），则点P平移后P′（2，2），将点P′绕原点顺时针旋转90°，则点M′（2，﹣2），将Q′（0，0）平移至点Q（t﹣2，t﹣3），则点M′平移后即为点M（t，t﹣5），∴，∴t1=4，t2=﹣2，∴M1（4，﹣1），M2（﹣2，﹣7）；

③当P为直角顶点时，同理可得M1（4，﹣1），M2（﹣2，﹣7），综上所述，所有符合条件的点M的坐标为：

M1（4，﹣1），M2（﹣2，﹣7），M3（，），M4（，）．

（ii）存在最大值．理由如下：

由（i）知PQ=为定值，则当NP+BQ取最小值时，有最大值．

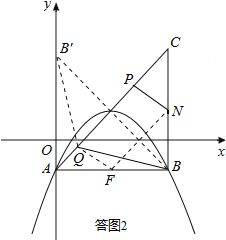
如答图2，取点B关于AC的对称点B′，易得点B′的坐标为（0，3），BQ=B′Q．

连接QF，FN，QB′，易得FN∥PQ，且FN=PQ，∴四边形PQFN为平行四边形，∴NP=FQ，∴NP+BQ=FQ+B′Q≥FB′==，∴当B′、Q、F三点共线时，NP+BQ最小，最小值为，∴的最大值为=．