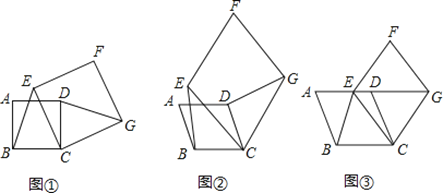
【题目】感知:如图①,四边形ABCD、CEFG均为正方形.易知BE=DG.
探究:如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.
应用:如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD的延长线上.若AE=3ED, ∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为 .
参考答案:
【答案】(1)证明见解析;(2)20
【解析】试题分析:探究:由四边形ABCD、四边形CEFG均为菱形,利用SAS易证得△BCE≌△DCG,则可得BE=DG;
应用:由AD∥BC,BE=DG,可得S△ABE+S△CDE=S△BEC=S△CDG=8,又由AE=3ED,可求得△CDE的面积,继而求得答案.
试题解析:
探究:∵四边形ABCD、四边形CEFG均为菱形,
∴BC=CD,CE=CG,∠BCD=∠A,∠ECG=∠F.
∵∠A=∠F,
∴∠BCD=∠ECG.
∴∠BCD-∠ECD=∠ECG-∠ECD,
即∠BCE=∠DCG.
在△BCE和△DCG中,
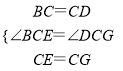
∴△BCE≌△DCG(SAS),
∴BE=DG.
应用:∵四边形ABCD为菱形,
∴AD∥BC,
∵BE=DG,
∴S△ABE+S△CDE=S△BEC=S△CDG=8,
∵AE=3ED,
∴S△CDE=![]() ,
,
∴S△ECG=S△CDE+S△CDG=10
∴S菱形CEFG=2S△ECG=20.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:(8x﹣7y)﹣2(4x﹣5y)
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(1,﹣2)关于y轴对称的点的坐标是( )
A. (1,2) B. (﹣1,2) C. (﹣1,﹣2) D. (﹣2,1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一条船在一条河上的顺流航速是逆流航速的3倍,这条船在静水中的航速与河水的流速之比为( )
A. 3:1 B. 2:1 C. 1:1 D. 3:2
-
科目: 来源: 题型:
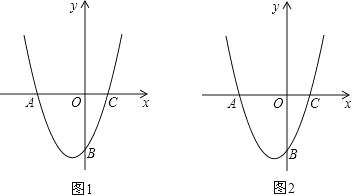
查看答案和解析>>【题目】在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)已知点D(m,m﹣2)在第三象限的抛物线上,求点D关于直线AB对称的点E的坐标;
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,求出相应点Q的坐标.
-
科目: 来源: 题型:
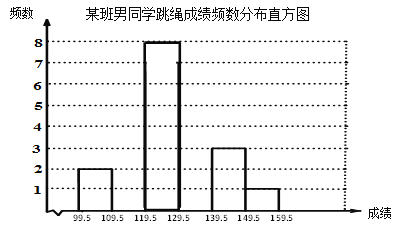
查看答案和解析>>【题目】我校八年级全体男同学参加了跳绳比赛.从中随机抽取某班男同学的跳绳成绩,制作了如下频数分布表:
组别
99.5﹣109.5
109.5﹣119.5
119.5﹣129.5
129.5﹣139.5
139.5﹣149.5
149.5﹣159.5
频数
2
4
8
7
3
1
根据上面统计信息,解答下列问题:
(1)补全频数分布直方图;
(2)班级准备对跳绳成绩优秀的男同学进行奖励,奖励人数占班级男同学的20%,该班张辉同学的成绩为140个,通过计算判断张辉能否获得奖励;
(3)八年级共有200名男同学,若规定男同学的跳绳成绩在120个以上(含120个)为合格,估计该校八年级男同学成绩合格的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小刚问妈妈的年龄,妈妈笑着说:“我们两人现在的年龄和为52岁,两年后我的年龄是你的年龄的2倍多2岁,你能用学过的知识求出我的年龄吗?”小刚想了一会,得出的正确结果是_____.
相关试题

