【题目】小明在某次作业中得到如下结果: sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°≈( ![]() )2+(
)2+( ![]() )2=1.
)2=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°﹣α)=1.
(Ⅰ)当α=30°时,验证sin2α+sin2(90°﹣α)=1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
参考答案:
【答案】解:(Ⅰ)当α=30°时, sin2α+sin2(90°﹣α)
=sin230°+sin260°
=( ![]() )2+(
)2+( ![]() )2
)2
= ![]() +
+ ![]()
=1;
(Ⅱ)小明的猜想成立,证明如下:
如图,在△ABC中,∠C=90°,
设∠A=α,则∠B=90°﹣α,
∴sin2α+sin2(90°﹣α)
=( ![]() )2+(
)2+( ![]() )2
)2
= ![]()
= ![]()
=1.
【解析】(1)将α=30°代入,根据三角函数值计算可得;(2)设∠A=α,则∠B=90°﹣α,根据正弦函数的定义及勾股定理即可验证.
【考点精析】本题主要考查了互余两角的三角函数关系和特殊角的三角函数值的相关知识点,需要掌握互余关系:sinA=cos(90°—A),cosA=sin(90°—A),tanA=cot(90°—A),cotA=tan(90°—A);分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,把矩形OABC沿对角线AC所在直线折叠,点B落在点D处,DC与y轴相交于点E,矩形OABC的边OC,OA的长是关于x的一元二次方程x2﹣12x+32=0的两个根,且OA>OC.

(1)求线段OA,OC的长;
(2)求证:△ADE≌△COE,并求出线段OE的长;
(3)直接写出点D的坐标;
(4)若F是直线AC上一个动点,在坐标平面内是否存在点P,使以点E,C,P,F为顶点的四边形是菱形?若存在,请直接写出P点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求作∠ABC的平分线,分别交AD,AD于P,Q两点;并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.
(Ⅰ)若AB=4,求 的长;
的长;
(Ⅱ)若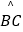 =
=  ,AD=AP,求证:PD是⊙O的切线.
,AD=AP,求证:PD是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数
0
1
2
3
4
5(含5次以上)
累计车费
0
0.5
0.9
a
b
1.5
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数
0
1
2
3
4
5
人数
5
15
10
30
25
15
(Ⅰ)写出a,b的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,AD=8,P,E分别是线段AC、BC上的点,且四边形PEFD为矩形.

(Ⅰ)若△PCD是等腰三角形时,求AP的长;
(Ⅱ)若AP= ,求CF的长.
,求CF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=2x+m与抛物线y=ax2+ax+b有一个公共点M(1,0),且a<b.
(Ⅰ)求抛物线顶点Q的坐标(用含a的代数式表示);
(Ⅱ)说明直线与抛物线有两个交点;
(Ⅲ)直线与抛物线的另一个交点记为N.
(ⅰ)若﹣1≤a≤﹣ ,求线段MN长度的取值范围;
,求线段MN长度的取值范围;
(ⅱ)求△QMN面积的最小值.
相关试题

