【题目】探究;
(![]() )如图,
)如图, ![]() 、
、![]() 为
为![]() 的边
的边![]() 、
、![]() 上的两定点,在
上的两定点,在![]() 上求作一点
上求作一点![]() ,使
,使![]() 的周长最短.(不写作法)
的周长最短.(不写作法)

(![]() )如图,矩形
)如图,矩形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,点
的中点,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的动点,求四边形
上的动点,求四边形![]() 周长的最小值.
周长的最小值.

(![]() )如图,正方形
)如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 为
为![]() 边中点,在边
边中点,在边![]() 、
、![]() 、
、![]() 上分别确定点
上分别确定点![]() 、
、![]() 、
、![]() .使得四边形
.使得四边形![]() 周长最小,并求出最小值.
周长最小,并求出最小值.

参考答案:
【答案】(1)作图见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】(1)
试题分析:(1)利用轴对称图形的性质,作点P关于BC的对称点P′,连接P′Q,交BC于点M,则M是所求的点;(2)如图,延长EB至E'使E' B=EB,延长FD至F'使F' D=FD,连接E' F'交BC、CD于M、N.此时四边形EFNM周长最小.根据勾股定理求得EF、E' F'的长,即可得四边形OMNP周长的最小值;(3)如图,延长![]() 到
到![]() 使
使![]() ,延长
,延长![]() 至
至![]() 使
使![]() .作
.作![]() 关于直线
关于直线![]() 对称的点
对称的点![]() ,连接
,连接![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]() .连
.连![]() 交
交![]() 于
于![]() ,即为周长最小.根据正方形的性质和轴对称的性质易得
,即为周长最小.根据正方形的性质和轴对称的性质易得![]() 、
、![]() 、
、![]() 为各边中点,所以四边形
为各边中点,所以四边形![]() 周长的最小值为
周长的最小值为![]() .
.
试题解析:
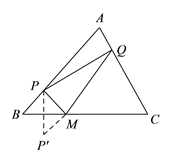
(![]() )如图,作点
)如图,作点![]() 关于
关于![]() 的对称点
的对称点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 是所求的点.
是所求的点.
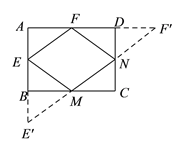
(![]() )如图,延长
)如图,延长![]() 至
至![]() 使
使![]() ,延长
,延长![]() 至
至![]() 使
使![]() ,连接
,连接![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]() .此时四边形
.此时四边形![]() 周长最小.
周长最小.
周长![]()
![]()
![]() .
.
(![]() )如图,延长
)如图,延长![]() 到
到![]() 使
使![]() ,延长
,延长![]() 至
至![]() 使
使![]() .
.
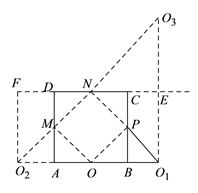
作![]() 关于直线
关于直线![]() 对称的点
对称的点![]() ,连接
,连接![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]() .
.
连![]() 交
交![]() 于
于![]() ,即为周长最小.
,即为周长最小.
易得![]() 、
、![]() 、
、![]() 为各边中点,周长为
为各边中点,周长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(﹣1,5)、B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解集为( )

A. ﹣1≤x≤9 B. ﹣1≤x<9 C. ﹣1<x≤9 D. x≤﹣1或x≥9
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列现象中:①时针转动,②电风扇叶片的转动,③转呼啦圈,④传送带上的电视机,其中是旋转的有( )
A.①②
B.②③
C.①④
D.③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】用数学的方式理解“当窗理云鬓,对镜贴花黄”和“坐地日行八万里”(只考虑地球的自转),其中蕴含的图形运动是( )
A.平移和旋转
B.对称和旋转
C.对称和平移
D.旋转和平移 -
科目: 来源: 题型:
查看答案和解析>>【题目】某种细胞的直径是0.000067厘米,将0.000067用科学记数法表示为( )
A.6.7×10﹣5
B.6.7×10﹣6
C.0.67×10﹣5
D.6.7×10﹣6 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级甲、乙两班举行电脑汉字输入比赛,两个班能参加比赛的学生每分钟输入汉字的个数,经统计和计算后结果如下表:

有一位同学根据上面表格得出如下结论:
①甲、乙两班学生的平均水平相同;②乙班优秀人数比甲班优秀人数多(每分钟输入汉字达150个以上为优秀);③甲班学生比赛成绩的波动比乙班学生比赛成绩的波动大.
上述结论正确的是_______(填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
相关试题

