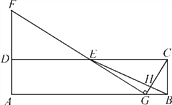
【题目】如图,在矩形ABCD中,E为CD的中点,H为BE上的一点, ![]() =3,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
=3,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
(1)求证: ![]() ;
;
(2)若∠CGF=90°,求![]() 的值.
的值.
参考答案:
【答案】(1)证明见解析;(2) ![]() =3
=3![]() .
.
【解析】试题分析:(1)根据相似三角形判定的方法,判断出△CEH∽△GBH,即可推得结论;
(2)作EM⊥AB于M,则EM=BC=AD,AM=DE,设DE=CE=3a,则AB=CD=6a,由(1)得: ![]() =3,得出BG=
=3,得出BG=![]() CE=a,AG=5a,证明△DEF∽△GEC,由相似三角形的性质得出EGEF=DEEC,由平行线证出
CE=a,AG=5a,证明△DEF∽△GEC,由相似三角形的性质得出EGEF=DEEC,由平行线证出![]() =
=![]() ,得出EF=
,得出EF=![]() EG,求出EG=
EG,求出EG=![]() a,在Rt△EMG中,GM=2a,由勾股定理求出BC=EM=
a,在Rt△EMG中,GM=2a,由勾股定理求出BC=EM=![]() a,即可得出结果.
a,即可得出结果.
试题解析:解:(1)∵四边形ABCD是矩形,∴CD∥AB,AD=BC,AB=CD,AD∥BC,∴△CEH∽△GBH,∴ ![]() .
.
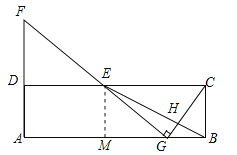
(2)作EM⊥AB于M,如图所示:
则EM=BC=AD,AM=DE,∵E为CD的中点,∴DE=CE,设DE=CE=3a,则AB=CD=6a,由(1)得: ![]() =3,∴BG=
=3,∴BG=![]() CE=a,∴AG=5a,∵∠EDF=90°=∠CGF,∠DEF=∠GEC,∴△DEF∽△GEC,∴
CE=a,∴AG=5a,∵∠EDF=90°=∠CGF,∠DEF=∠GEC,∴△DEF∽△GEC,∴![]() ,∴EGEF=DEEC,∵CD∥AB,∴
,∴EGEF=DEEC,∵CD∥AB,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴EF=
,∴EF=![]() EG,∴EG
EG,∴EG![]() EG=3a3a,解得:EG=
EG=3a3a,解得:EG=![]() a,在Rt△EMG中,GM=2a,∴EM=
a,在Rt△EMG中,GM=2a,∴EM=![]() =
=![]() a,∴BC=
a,∴BC=![]() a,∴
a,∴![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列因式分解正确的是( )
A. x2+2x-1=(x-1)2 B. a2-a=a(a+1)
C. m2+(-n)2=(m+n)(m-n) D. -9+4y2=(3+2y)(2y-3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】正五边形的每个内角度数是( )
A. 60° B. 90° C. 108° D. 120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中是必然发生的事件是( )
A.投掷一枚质地均匀的骰子,掷得的点数是奇数;
B.某种彩票中奖率是1%,则买这种彩票100张一定会中奖;
C.掷一枚硬币,正面朝上 ;
D.任意画一个三角形,其内角和是180° .
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一个外角为140°,那么底角等于( )
A、40° B、100° C、70° D、40°或70°
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一箱规格相同的红、黄两种颜色的小塑料球共1000个.为了估计这两种颜色的球各有多少个,小明将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后.发现摸到红球的频率约为0.6,据此可以估计红球的个数约为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:(3x2﹣xy+y)﹣2(5xy﹣4x2+y),其中x=2,y=﹣1.
相关试题

