【题目】如果点M、N在数轴上分别表示实数m,n,在数轴上M,N两点之间的距离表示为MN=m-n(m>n)或n-m(m<n)或︱m-n︱.利用数形结合思想解决下列问题:
已知数轴上点A与点B的距离为16个单位长度,点A在原点的左侧,到原点的距离为26个单位长度,点B在点A的右侧,点C表示的数与点B表示的数互为相反数,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)点A表示的数为___________,点B表示的数为___________,点C表示的数为___________.
(2)用含t的代数式表示P到点A和点C的距离: PA= ,PC=___________.
(3)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动, Q点到达C点后,再立即以同样的速度返回,运动到终点A.
①在点Q向点C运动过程中,能否追上点P?若能,请求出点Q运动几秒追上.
②在点Q开始运动后,P、Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由.
![]()
参考答案:
【答案】(1)-26,-10,10;(2)t,36-t;(3)-3,-1,3.5
【解析】试题分析:
(1)由点A在原点的左侧,到原点的距离为26个单位长度,可知点A表示的数为-26,根据点B在点A的右侧,点A与点B的距离为16个单位长度,得出点B表示的数为-10,由点C表示的数与点B表示的数互为相反数,得到点C表示的数为10;
(2)根据列出=速度×时间,可得PA=1×t=t,由PC=AC-PA可得PC=36-t;
(3)①在点Q向点C运动过程中,设点Q运动x秒追上点P,根据点Q追上点P时,点Q运动的路程=点P运动的路程,列出方程,解方程即可;
②分两种情况:点Q从A点向点C运动时,又分点Q在点P的后面与点Q在点P的前面;点Q从C点返回到点A时,又分点Q在点P的后面与点Q在点P的前面.
试题解析:(1)∵点A在原点的左侧,到原点的距离为26个单位长度,
∴点A表示的数为-26,
∵点A与点B的距离为16个单位长度,且点B在点A的右侧,
∴点B表示的数为-26+16=-10,
∵点C表示的数与点B表示的数互为相反数,
∴点C表示的数为10.
(2)PA=1×t=t,
PC=AC-PA=36-t.
(3)①在点Q向点C运动过程中,设点Q运动x秒追上点P,根据题意得
3x=x+16,
解得x=8.
答:在点Q向点C运动过程中,能追上点P,点Q运动8秒追上;
②分两种情况:
(Ⅰ)点Q从A点向点C运动时,
如果点Q在点P的后面,那么1x+16-3x=2,解得x=7,此时点P表示的数是-3;
如果点Q在点P的前面,那么3x-(1x+16)=2,解得x=9,此时点P表示的数是-1;
(Ⅱ)点Q从C点返回到点A时,
如果点Q在点P的后面,那么3x+1x+16+2=2×36,解得x=![]() ,此时点P表示的数是
,此时点P表示的数是![]() ;
;
如果点Q在点P的前面,那么3x+1x+16=2×36+2,解得x=![]() ,此时点P表示的数是
,此时点P表示的数是![]() .
.
答:在点Q开始运动后,P、Q两点之间的距离能为2个单位,此时点P表示的数分别是-3,-1, ![]() ,
, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在实施“中小学校舍安全工程”之际,某市计划对
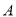 、
、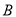 两类学校的校舍进行改造,根据预算,改造一所
两类学校的校舍进行改造,根据预算,改造一所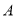 类学校和三所
类学校和三所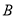 类学校的校舍共需资金480万元,改造三所
类学校的校舍共需资金480万元,改造三所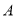 类学校和一所
类学校和一所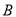 类学校的校舍共需资金400万元.
类学校的校舍共需资金400万元.(1)改造一所
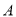 类学校的校舍和一所
类学校的校舍和一所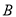 类学校的校舍所需资金分别是多少万元?
类学校的校舍所需资金分别是多少万元?(2)该市某县
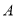 、
、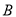 两类学校共有8所需要改造.改造资金由国家财政和地方财政共同承担,若国家财政拨付的改造资金不超过770万元,地方财政投入的资金不少于210万元,其中地方财政投入到
两类学校共有8所需要改造.改造资金由国家财政和地方财政共同承担,若国家财政拨付的改造资金不超过770万元,地方财政投入的资金不少于210万元,其中地方财政投入到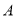 、
、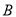 两类学校的改造资金分别为每所20万元和30万元,请你通过计算求出有几种改造方案,每个方案中
两类学校的改造资金分别为每所20万元和30万元,请你通过计算求出有几种改造方案,每个方案中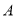 、
、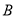 两类学校各有几所.
两类学校各有几所. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一组实数,
 ,
,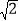 ,
, , 1+
, 1+ ,
,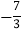 ,
,
(1)将它们分类,填在相应的括号内:
有理数{ … };
无理数{ …};
(2)请你选出2个有理数和2个无理数, 再用 “+,-,×,÷” 中的3种不同的运算符号将选出的4个数进行运算(可以用括号), 使得运算的结果是一个正整数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个三角形相似,其中一个三角形的两个内角是40°、60°.那么另一个三角形的最大角是________度,最小角是________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图反映的是小刚从家里跑步去体育馆,在哪里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小刚离家的距离.
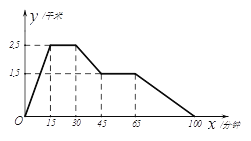
根据图象回答下列问题:
(1)体育场离陈欢家______千米,小刚在体育场锻炼了________分钟.
(2)体育场离文具店_________千米,小刚在文具店停留了________分钟.
(3)小刚从家跑步到体育场、从体育场走到文具店、从文具店散步回家的速度分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各点中,在正比例函数y=3x的图象上的是( )
A.(1,3)B.(﹣1,3)C.(3,1)D.(3,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】-1, 0, 2.5,+34 ,-1.842,-3.14,2036,-127 中,正数有_______,负数有_______.
相关试题

