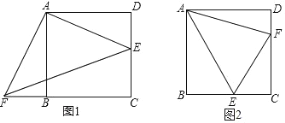
【题目】如图1,四边形ABCD是正方形,△ADE经旋转后与△ABF重合.
(1)旋转中心是 ;旋转角是 度; 如果连接EF,那么△AEF是 三角形.
(2)用上述思想或其他方法证明:如图2,在正方形ABCD中,点E、F分别在BC、CD上,且∠EAF=45°.
求证:EF=BE+DF.
(3)若DF=4,EF=10,求四边形AECD的面积。
参考答案:
【答案】(1)△AEF是等腰直角三角形(2)证明见解析(3)108
【解析】试题分析:(1)△ADE经旋转后与△ABF重合,所以旋转中心为点A,因为四边形ABCD是正方形,所以∠BAD=90°,所以旋转角为90°,由旋转得AE=AF,所以△AEF是等腰直角三角形;(2)利用第一问的旋转的思想来证明即可;(3)根据第二问的结论,可以求出正方形的边长,从而求出正方形的面积.
试题解析:
(1)旋转中心是点A,旋转角=∠DAB=90°,△AEF是等腰直角三角形;
(2)如图所示,将△ABE绕A点逆时针旋转90°,得到△ADE′,
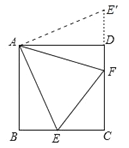
因为∠EAF=45°,
所以∠BAE+∠DAF=45°,
因为∠BAE=∠DAE′,
所以∠FAE′=45°,
所以∠FAE′=∠FAE,
因为∠ADE′=∠ADF=90°,
所以E'、D、F三点共线,
又因为AF=AF,AE=AE′,
所以△EAF≌△E′AF(SAS),
所以EF=E′F,
因为E′F=DF+DE′,E′D=BE,
所以EF=BE+DF.
(3)108
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).
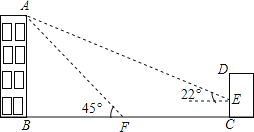
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈
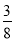 ,cos22°≈
,cos22°≈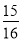 ,tan22°≈
,tan22°≈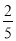 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】将一元二次方程3x2﹣1=4x化成一般形式为( )
A.3x2+4x=1
B.3x2﹣4x=1
C.3x2﹣4x﹣1=0
D.3x2+4x﹣1=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】小惠在纸上画了一条数轴后,折叠纸面,使数轴上表示1的点与表示﹣3的点重合,若数轴上A,B两点之间的距离为2014(A在B的左侧),且A,B两点经上述折叠后重合,则A点表示的数为( )
A.﹣1006
B.﹣1007
C.﹣1008
D.﹣1009 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知坐标平面内的三个点A,B,O.
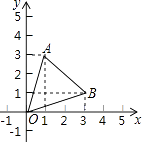
(1)写出点O坐标 , 点A坐标 , 点B坐标;
(2)求△ABO的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x﹣2y+3=0,则代数式﹣2x+4y+2017的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若“★”是新规定的某种运算符号,设a★b=ab+a﹣b,则2★n=﹣8,则n= .
相关试题

