【题目】如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=![]() (k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(1)求该双曲线所表示的函数解析式;
(2)求等边△AEF的边长.

参考答案:
【答案】解:(1) 过点C作CG⊥OA于点G,

∵点C是等边△OAB的边OB的中点,
∴OC=2,∠ AOB=60°。∴OG=1,CG=![]() ,
,
∴点C的坐标是(1, ![]() )。由
)。由![]() ,得:k=
,得:k=![]() 。
。
∴该双曲线所表示的函数解析式为![]() 。
。
(2) 过点D作DH⊥AF于点H,设AH=a,则DH=![]() a。
a。
∴点D的坐标为(4+a, ![]() a)。
a)。
∵点D是双曲线![]() 上的点,
上的点,
∴由xy=![]() ,得
,得![]() a (4+a)=
a (4+a)=![]() ,即:a2+4a-1=0。
,即:a2+4a-1=0。
解得:a1=![]() -2,a2=-
-2,a2=-![]() -2(舍去)。∴AD=2AH=2
-2(舍去)。∴AD=2AH=2![]() -4。
-4。
∴等边△AEF的边长是2AD=4![]() -8。.
-8。.
【解析】(1)过点C作CG⊥OA于点G,根据等边三角形的性质求出OG、CG的长度,从而得到点C的坐标,再利用待定系数法求反比例函数解析式列式计算即可得解。
(2)过点D作DH⊥AF于点H,设AH=a,根据等边三角形的性质表示出DH的长度,然后表示出点D的坐标,再把点D的坐标代入反比例函数解析式,解方程得到a的值,从而得解。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是( )

A.4
B.2
C.4
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四人进行射击测试,每人10次射击成绩平均数均是9.2环,方差分别为S甲2=0.56,S乙2=0.60,S丙2=0.50,S丁2=0.45,则成绩最稳定的是( )
A.甲
B.乙
C.丙
D.丁 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EG⊥CD于点G,则∠FGC= .
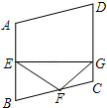
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)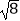 +|1﹣
+|1﹣  |﹣π0+(
|﹣π0+(  )﹣1
)﹣1
(2)(2 ﹣2
﹣2  )(
)( 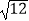 +
+ 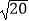 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:|x|=2,|y|=3,且x>y,则x+y的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不能镶嵌成平面图案的正多边形组合为( )
A.正八边形和正方形
B.正五边形和正十边形
C.正六边形和正三角形
D.正六边形和正八边形
相关试题

