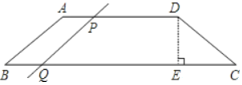
【题目】如图,在四边形ABCD中,AD∥BC,AB=CD,DE⊥BC于点E,且DE=![]() ,AD=18,∠C=60°;
,AD=18,∠C=60°;
(1)BC=________
(2)若动点P从点D出发,速度为2个单位/秒,沿DA向点A运动,同时,动点Q从点B出发,速度为3个单位/秒,沿BC向点C运动,当一个动点到达端点时,另一个动点同时停止运动,设运动的时间为t秒。
①t=_______秒时,四边形PQED是矩形;
②t为何值时,线段PQ与四边形ABCD的边构成平行四边形;
③是否存在t值,使②中的平行四边形是菱形?若存在,请求出t值,若不存在,请说明理由。
参考答案:
【答案】(1)26;(2)①![]() ;②当t=
;②当t=![]() 或
或![]() 时,,线段PQ与四边形ABCD的边构成平行四边形;③不存在t值,使②中的平行四边形是菱形,理由详见解析.
时,,线段PQ与四边形ABCD的边构成平行四边形;③不存在t值,使②中的平行四边形是菱形,理由详见解析.
【解析】
(1)先在Rt△DEC中利用特殊三角函数值可求CE,进而可求CD,再利用等腰梯形的性质可求BC;(2)①先画图,由于四边形PQED是矩形,那么矩形的对边相等,于是PD=QE,再根据路程=速度×时间,可得2t=26-4-3t,进而可求t;②有两种情况:(i)是PQ与AB构成平行四边形,根据平行四边形的性质,对边相等,可得AP=BQ,再根据路程=速度×时间,可得3t=18-2t,进而可求t; (ii)是PQ与CD构成平行四边形,根据平行四边形的性质,对边相等,可得PD=CQ,再根据路程=速度×时间,可得2t=26-3t,进而可求t;③根据②中的两种情况,分别求出BQ、DP的值,再与邻边AB、CD比较,从而可判断不存在t值,使②中的平行四边形是菱形.
∵DE⊥BC,
∴∠DEC=90°,
又∵∠C=60°,
∴CE=![]() =4,∠EDC=30°,
=4,∠EDC=30°,
∴CD=2CE=8,
∵AD∥BC,AB=CD,
∴四边形ABD是等腰梯形,
∴BC=2CE+AD=8+18=26;
故答案为:26;
(2)①设运动时间为t时,四边形PQED是矩形,如图,
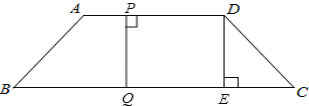
∵四边形PQED是矩形,
∴PD=QE,
∴2t=26-4-3t,
解得t=![]() ;
;
故答案为:![]() ;
;
②有两种情况:
(i)设运动时间为t时,线段PQ与AB构成平行四边形,如图,
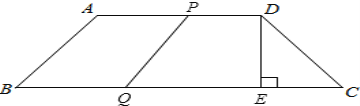
∵四边形ABQP是平行四边形,
∴AP=BQ,
∴3t=18-2t,
解得t=![]() ,
,
(ii)设运动时间为t时,线段PQ与CD构成平行四边形,如图,
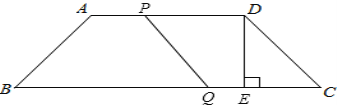
∵四边形PQCD是平行四边形,
∴PD=CQ,
∴2t=26-3t,
解得t=![]() ,
,
综上,当t=![]() 或
或![]() 时,,线段PQ与四边形ABCD的边构成平行四边形;
时,,线段PQ与四边形ABCD的边构成平行四边形;
③不存在t值,使②中的平行四边形是菱形,
(i)当t=![]() 时,BQ=3t=
时,BQ=3t=![]() ,
,
而AB=CD=8,
所以BQ≠AB,
∴四边形ABQP不是菱形,
(ii)当t=![]() 时,DP=2t=
时,DP=2t=![]() ,
,
而AB=CD=8,
所以DP≠AB,
∴四边形PQCD不是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学库存若干套桌椅,准备修理后支援贫困山区学校。现有甲、乙两木工组,甲每天修理桌椅16套,乙每天修桌椅比甲多8套,甲单独修完这些桌椅比乙单独修完多用20天,学校每天付甲组80元修理费,付乙组120元修理费。
(1)该中学库存多少套桌椅?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:a、由甲单独修理;b、由乙单独修理;c、甲、乙合作同时修理。你认为哪种方案省时又省钱?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一出租车一天下午以银泰城为出发地,在东西走向的马路上营运,如果规定向东行驶为正,行车里程(单位:
 )依先后次序记录如下:
)依先后次序记录如下: ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, .
. (1)将最后一名乘客送到目的地,出租车离银泰城出发点多远?在银泰城的什么方向?
(2)若每千米的价格为
 元,司机一个下午的营业额为多少?
元,司机一个下午的营业额为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且AE=BD,
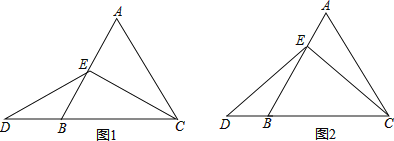
(1)当点E为AB的中点时,如图1,求证:EC=ED;
(2)当点E不是AB的中点时,如图2,过点E作EF//BC,求证:△AEF是等边三角形;
(3)在第(2)小题的条件下,EC与ED还相等吗,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,中俄“海上联合—2017”军事演习在海上编队演习中,两艘航母护卫舰从同一港口O同时出发,一号舰沿南偏西30°方向以12海里/小时的速度航行,二号舰以16海里/小时速度航行,离开港口1.5小时后它们分别到达A,B两点,相距30海里,则二号舰航行的方向是( )

A. 南偏东30° B. 北偏东30° C. 南偏东 60° D. 南偏西 60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己知正方形ABCD的边长为4, P是对角线BD上一点,PE⊥BC于点E, PF⊥CD于点F,连接AP, EF.给出下列结论:①PD=
 EC:②四边形PECF的周长为8;③△APD一定是等腰三角形:④AP=EF;⑤EF的最小值为
EC:②四边形PECF的周长为8;③△APD一定是等腰三角形:④AP=EF;⑤EF的最小值为 ;⑥AP⊥EF.其中正确结论的序号为( )
;⑥AP⊥EF.其中正确结论的序号为( )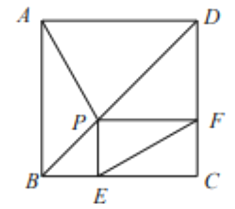
A. ①②④⑤⑥B. ①②④⑤
C. ②④⑤D. ②④⑤⑥
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空,完成下列说理过程.
如图,点
 、
、 、
、 在同一条直线上,
在同一条直线上, ,
, 分别平分
分别平分 和
和 .
.
(1)求
 的度数:
的度数:(2)如果
 ,求
,求 的度数.
的度数.解:(1)如图,因为
 是
是 的平分线,
的平分线,所以
 .
.因为
 是
是 的平分线,
的平分线,所以
 ① .
① .所以
 ②
②  ③
③  .
.(2)由(1)可知
 .
.因为

所以 ④

则:
 ⑤
⑤  ⑥
⑥  .
.
相关试题

