【题目】如图,在ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC.求证:∠BAC=∠BFC. 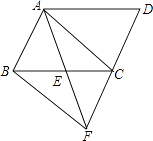
参考答案:
【答案】证明:∵四边形ABCD是平行四边形, ∴AB∥CD,
∵点F为DC的延长线上的一点,
∴AB∥DF,
∴∠BAE=∠CFE,∠ECF=∠EBA,
∵E为BC中点,
∴BE=CE,
在△BAE和△CFE中, 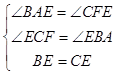 ,
,
∴△BAE≌△CFE,
∴AB=CF,
又∵AB∥CF,
∴四边形ABFC是平行四边形,
∴∠BAC=∠BFC.
【解析】根据平行四边形的性质可得到AB∥CD,从而可得到AB∥DF,得出∠BAE=∠CFE,∠ECF=∠EBA,由AAS证明△BAE≌△CFE,根据全等三角形的对应边相等可证得AB=CF,证出四边形ABFC是平行四边形,即可得出结论.
【考点精析】本题主要考查了平行四边形的性质的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别延长ABCD的边CD,AB到E,F,使DE=BF,连接EF,分别交AD,BC于G,H,连结CG,AH.
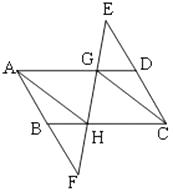
求证:CG∥AH. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣2x+k=0有实数根,则k的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、O、E在同一直线上,∠AOB=40°,∠COD=28°,OD平分∠COE.
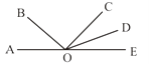
(1)求∠COB的度数;
(2)求∠AOD的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件是确定事件的是( )
A、阴天一定会下雨
B、黑暗中从5把不同的钥匙中随意摸出一把,用它打开了门
C、打开电视机,任选一个频道,屏幕上正在播放新闻联播
D、在五个抽屉中任意放入6本书,则至少有一个抽屉里有两本书
-
科目: 来源: 题型:
查看答案和解析>>【题目】能够找到一点,使该点到各边的距离相等的为( )①平行四边形;②菱形;③矩形;④正方形.
A.①与②B.②与③C.②与④D.③与④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E,F分别是AB,CD的中点,G,H分别是AF,CE的中点,连结EG,FH.
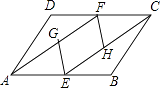
(1)四边形EHFG是不是平行四边形?如果是,请给出证明;如果不是,请说明理由;
(2)求四边形EHFG的面积与平行四边形ABCD的面积之比.
相关试题

