【题目】在△ABC中,AB=BC,∠ABC=45°,AD是BC边上的高,E是AD上一点,ED=CD,连接EC,
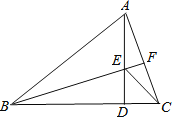
求证:
(1)△ADC≌△BDE;
(2)EA=EC.
参考答案:
【答案】见解析
【解析】
试题分析:(1)直接利用全等三角形的判定方法得出答案;
(2)由条件可求得∠BAC=∠BCA=67.5°,且∠BAD=∠DCE=45°,可得∠EAC=∠ECA=22.5°,可证得结论.
证明:(1)∵AD⊥BC,∠ABC=45°,
∴AD=BD,
在△ADC和△BDE中,
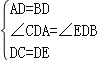 ,
,
∴△ADC≌△BDE(SAS);
(2)∵BA=BC,∠ABC=45°,
∴∠BCA=∠BAC=![]() ×135°=67.5°,
×135°=67.5°,
又∵AD⊥BC,
∴∠ADC=90°,
∵ED=CD,
∴∠ECD=45°,
∴∠ACE=67.5°﹣45°=22.5°,
∵∠AEC=∠EDC+∠ECD=135°,
∴∠EAC=180°﹣22.5°﹣135°=22.5°,
∴EA=EC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为太阳伞示意图,当伞收紧时,点P与点A重合,当伞慢慢撑开时,动点P由A向B移动;当点P到过点B时,伞张得最开.已知伞在撑开的过程中,总有PM=PN=CM=CN.则下列说法错误的是( )
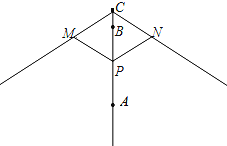
A.四边形PNCM可能会出现为正方形
B.四边形PNCM的周长始终不变
C.当∠CPN=60°时,CP=AP
D.四边形PNCM的面积始终不变
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b=3,ab=2,计算:a2b+ab2等于_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5人.”对于甲、乙两人的说法,有下列命题,其中是真命题的是( )
A. 若甲对,则乙对 B. 若乙对,则甲对
C. 若乙错,则甲错 D. 若甲错,则乙对
-
科目: 来源: 题型:
查看答案和解析>>【题目】判断下列命题是真命题还是假命题,如果是假命题,请举出一个反例.
(1)如果一个数是偶数,那么这个数是4的倍数.
(2)两个负数的差一定是负数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据报道,2014年4月昆明库塘蓄水量为58500万立方米,将58500万立方米用科学记数法表示为 万立方米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列命题:①三角形的两边之和大于第三边;②相等的角是对顶角;③若a与b互为倒数,则ab=1;④绝对值等于本身的数是正数.其中真命题的个数是( )
A. 1 B. 2 C. 3 D. 4
相关试题

