搜索
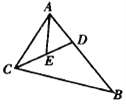
【题目】如图，在△ABC中，∠BAC=60°，BC=18，D是AB上一点，AC=BD，E是CD的中点.则AE的长是( ).
A. 12 B. 9 C. 9
D. 以上都不对
参考答案：
【答案】B
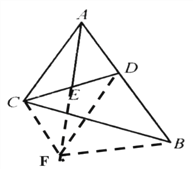
【解析】试题分析：如图所示，过D作DF∥AC，交AE的延长线于F，连接BF，CF，由此可得△DEF≌△CEA，根据全等三角形的性质可得AE=EF，因此可根据对角线互相平分的四边形是平行四边形，可得四边形ACFD是平行四边形，可得AC=DF，∠FDB=∠BAC=60°，∠ACF=120°，然后根据AC=BD，可得△DBF是等边三角形，可得AC=DF=DB=FB,∠BFC=120°，所以△ACF≌△BFC，因此可知BC=AF=2AE=18，解得AE=9.
故选：B
-
科目： 来源： 题型：
查看答案和解析>>【题目】在我们所学的课本中，多项式与多项式相乘可以用几何图形的面积来表示.例如，（2a+b）（a+b）=2a2+3ab+b2就可以用图（1）来表示.请你根据此方法写出图（2）中图形的面积所表示的代数恒等式：____________.
【答案】（a+2b）（2a+b）=2a2+5ab+2b2
【解析】试题分析：图②的面积可以用长为a+a+b，宽为b+a+b的长方形面积求出，也可以由四个正方形与5个小长方形的面积之和求出，表示出即可．
解：根据图形列得：（a+2b）（2a+b）=2a2+5ab+2b2．
故答案为：（a+2b）（2a+b）=2a2+5ab+2b2．
考点：多项式乘多项式．
点评：此题考查了多项式乘以多项式法则，熟练掌握法则是解本题的关键．
【题型】填空题
【结束】
18【题目】若一个正整数能表示为两个正整数的平方差，则称这个正整数为“智慧数”（如3=22-12，16=52-32，则3和16是智慧数）.已知按从小到大的顺序构成如下数列：3，5，7，8，9，11，12，13，15，16，17，19，20，21，23，24，25，…则第2 013个“智慧数”是______.
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列事件为必然事件的是（ ）．
A.画一个四边形，其内角为180°
B.用长度分别是4，6，9的三条线段能围成一个三角形
C.NBA球员库里罚篮两罚全中
D.在200个白球中放入1个红球，摇匀后随机摸出1球就摸出了红球
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列是假命题的是（ ）．
A.直角都相等B.同角的余角相等
C.相等的角是对顶角D.过直线外一点，有且只有一条直线与已知直线平行
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义：若点P（a，b）在函数y=
的图象上，将以a为二次项系数，b为一次项系数构造的二次函数y=ax2+bx称为函数y=
的一个“派生函数”．例如：点（2， 
）在函数y=
的图象上，则函数y=2x2+ 
称为函数y=
的一个“派生函数”．现给出以下两个命题：（1）存在函数y=
的一个“派生函数”，其图象的对称轴在y轴的右侧（2）函数y=
的所有“派生函数”的图象都经过同一点，下列判断正确的是（ ）A. 命题（1）与命题（2）都是真命题
B. 命题（1）与命题（2）都是假命题
C. 命题（1）是假命题，命题（2）是真命题
D. 命题（1）是真命题，命题（2）是假命题
-
科目： 来源： 题型：
查看答案和解析>>【题目】平面直角坐标系中，将点A（1，﹣2）向上平移1个单位长度后与点B重合，则点B的坐标是（________）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】方程3x+6=2x-8移项后,正确的是（ ）
A.3x+2x=6-8
B.3x-2x=-8+6
C.3x-2x=-6-8
D.3x-2x=8-6
相关试题
