搜索
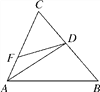
【题目】如图，在△ABC中，AD平分∠CAB，点F在边AC上，若∠CAB＋∠BDF＝180°.求证：DF＝DB.
参考答案：
【答案】见解析.
【解析】在AB上截取AE＝AF，根据角平分线和公共边得出△ADF和△ADE全等，从而得出DF=DE，根据∠CAB＋∠BDF＋∠5＋∠B＝360°，∠CAB＋∠BDF＝180°，得出∠5＋∠B＝180°，根据平角的性质以及∠5=∠3得出∠B=∠4，从而得出答案．
解：如图，在AB上截取AE＝AF，∵AD平分∠CAB，∴∠1＝∠2，
在△ADF和△ADE中，AF=AE，∠1=∠2，AD=AD，∴△ADF≌△ADE(SAS)，
∴DF＝DE，∠5＝∠3，∵∠CAB＋∠BDF＋∠5＋∠B＝360°，∠CAB＋∠BDF＝180°，
∴∠5＋∠B＝180°， 又∵∠3＋∠4＝180°，∠5＝∠3， ∴∠B＝∠4，
∴DB＝DE， ∴DF＝DB．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是某月的月历，用带阴影的方框任意框九个数。
（1）图中带阴影的方框中的9个数之和与方框正中心的数有什么关系？请说明你的理由？
（2）若这9个数之和是81，你能说出这9个日期吗？只要回答能或不能，且说明为什么？
（3）这9个数之和可能会是100吗？如果可能，请计算出这9个日期，如果不可能，请说明为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】暑假期间，七（2）班的张明、王强等同学随家长一同到某公园游玩，下面是购买门票时，张明与他爸爸的对话（如图），试根据图中的信息，解答下列问题：
⑴张明他们一共去了几个成人，几个学生？
⑵请你帮助张明算一算，用哪种方式购票(团体购票还是非团体购票)更省钱？说明理由.
⑶正要购票时，张明发现七（3）班的张小毛等15名同学和他们的2名家长共17人也来购票，请你为他们设计出最省的购票方案，并求出此时的购票费用.
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两果园分别产有苹果10吨和40吨，现全部运送到A、B两地销售，根据市场调研，A、B两地分别需要苹果15吨和35吨；已知从甲、乙地到A、B地的运价如表，由以上信息，解决下列问题：
到A地运价
到B地运价
甲果园
150元∕吨
120元∕吨
乙果园
100元∕吨
90元∕吨
（1）若从乙果园运到A地的苹果为
吨，则从甲果园运到B地的苹果为 吨；从甲果园将苹果运往A地的运输费用为 元（用含的代数式表示）；（2）若运往A地的运输费用比运往B地的运输费用少1150元，用你所学的知识来说明是怎样安排运输方案的？
-
科目： 来源： 题型：
查看答案和解析>>【题目】经营某种品牌的玩具，购进时的单价是30元，根据市场调查：在一段时间内，销售单价是40元时，销售量是600件，而销售单价每涨1元，就会少售出10件玩具．
（1）不妨设该种品牌玩具的销售单价为x元（x＞40），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在下列横线上： 销售单价x（元）；
销售量y（件）；
销售玩具获得利润w（元）；
（2）在（1）问条件下，若商场获得了10000元销售利润，求该玩具销售单价x应定为多少元．
（3）在（1）问条件下，若玩具厂规定该品牌玩具销售单价不低于44元，且商场要完成不少于540件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=﹣x2﹣2x+3 的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点．
（1）求A、B、C的坐标；
（2）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N．若点P在点Q左边，当矩形PMNQ的周长最大时，求△AEM的面积；
（3）在（2）的条件下，当矩形PMNQ的周长最大时，连接DQ．过抛物线上一点F作y轴的平行线，与直线AC交于点G（点G在点F的上方）．若FG=2
DQ，求点F的坐标． -
科目： 来源： 题型：
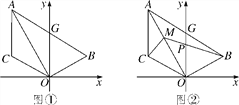
查看答案和解析>>【题目】如图①，已知线段AC∥y轴，点B在第一象限，且AO平分∠BAC，AB交y轴于G，连接OB，OC.
(1)判断△AOG的形状，并予以证明；
(2)若点B，C关于y轴对称，求证：AO⊥BO；
(3)在(2)的条件下，如图②，点M为OA上一点，且∠ACM＝45°，BM交y轴于P，若点B的坐标为(3，1)，求点M的坐标．
相关试题
