【题目】如图,在ABCD中,对角线AC、BD相交于点O,点E是AD的中点,如果OE=2,AD=6,那么ABCD的周长是( )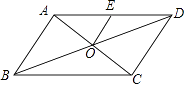
A.20
B.12
C.24
D.8
参考答案:
【答案】A
【解析】∵ABCD对角线相交于点O,E是AD的中点,
∴AB=CD,AD=BC=6,EO是△ABD的中位线,
∴AB=2OE=4,
∴ABCD的周长=2(AB+AD)=20.
所以答案是:A.
【考点精析】关于本题考查的三角形中位线定理和平行四边形的性质,需要了解连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能得出正确答案.
-
科目: 来源: 题型:
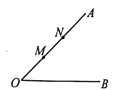
查看答案和解析>>【题目】如图,∠AOB=45°,点M、N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P、M、N构成等腰三角形的点P恰好有三个,则x的值是 .
-
科目: 来源: 题型:
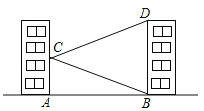
查看答案和解析>>【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(1)求∠BCD的度数.
(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣15﹣(﹣4)+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(﹣2ab+3a)﹣2(2a﹣b)+2ab,其中a=3,b=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC与BD交于点O,下列条件中不一定能判定这个四边形是平行四边形的是( )
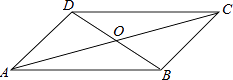
A.AB∥DC,AD=BC
B.AD∥BC,AB∥DC
C.AB=DC,AD=BC
D.OA=OC,OB=OD -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD;
(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形,求AE的长.

相关试题

