【题目】直线AB与x轴交于点A(2,0),与y轴交于点B(0,-4).
(1)求直线AB的解析式。
(2)若直线CD与AB平行,且直线CD与y轴的交点与B点相距2个单位,则直线CD的解析式为。
参考答案:
【答案】
(1)解:设 ![]()
由题意得 ![]() ,
, ![]()
解得 ![]()
![]()
(2)![]() 或
或 ![]()
【解析】(1)利用待定系数法,设一次函数的解析式为 y = k x + b ( k ≠ 0 ) ,且图象经过点A(2,0)与点B(0,-4),代入解析式中解方程求得即可;(2)根据直线CD与AB平行,因此两条直线的“k”值相同,再根据直线CD与y轴的交点与B点相距2个单位,即y=2x-4![]() 2,进而得出直线CD的解析式.
2,进而得出直线CD的解析式.![]()
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米.
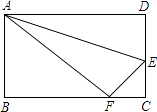
(1)BF=厘米;
(2)求EC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知二次函数
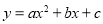 (a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为
(a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为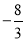 ,直线l的解析式为y=x.
,直线l的解析式为y=x.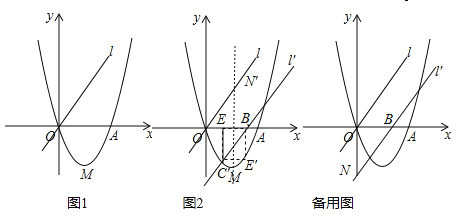
(1)求二次函数的解析式;
(2)直线l沿x轴向右平移,得直线l′,l′与线段OA相交于点B,与x轴下方的抛物线相交于点C,过点C作CE⊥x轴于点E,把△BCE沿直线l′折叠,当点E恰好落在抛物线上点E′时(图2),求直线l′的解析式;
(3)在(2)的条件下,l′与y轴交于点N,把△BON绕点O逆时针旋转135°得到△B′ON′,P为l′上的动点,当△PB′N′为等腰三角形时,求符合条件的点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简9a﹣5a的结果是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a﹣b=﹣3,c+d=2,则(b+c)﹣(a﹣d)的值为( )
A.﹣1
B.﹣5
C.5
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段能组成三角形的是( )
A. 1,2,4 B. 3,5,8 C. 5,5,11 D. 4,9,6
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:ab﹣a= .
相关试题

