【题目】解答
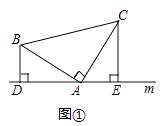
(1)已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,求证:DE=BD+CE. 
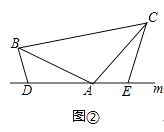
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明:若不成立,请说明理由. 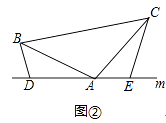
参考答案:
【答案】
(1)证明:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
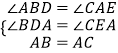 ,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE
(2)证明:∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
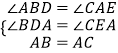 ,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE
【解析】(1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA,
则AE=BD,AD=CE,于是DE=AE+AD=BD+CE;(2)利用∠BDA=∠BAC=α,则∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,得出∠CAE=∠ABD,进而得出△ADB≌△CEA即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为
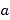 的菱形ABCD的顶点D在反比例函数
的菱形ABCD的顶点D在反比例函数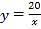 (
(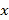 >0)的图象上,A点的坐标为(0,4),连接BD,交
>0)的图象上,A点的坐标为(0,4),连接BD,交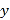 轴于点P.
轴于点P.(1)求菱形边长
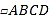 及点C坐标;
及点C坐标;(2)
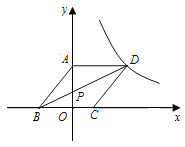 沿着线段BD平移,当点C落在
沿着线段BD平移,当点C落在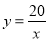 (
(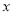 >0)上时,求点B沿BD方向移动的距离.
>0)上时,求点B沿BD方向移动的距离.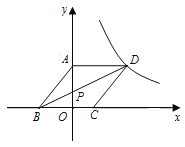
-
科目: 来源: 题型:
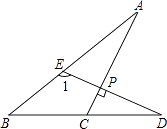
查看答案和解析>>【题目】如图,已知∠A=20°,∠B=27°,AC⊥DE,求∠1,∠D的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H.求证:
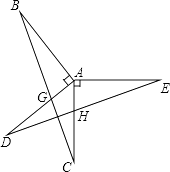
(1)△ABC≌△ADE;
(2)BC⊥DE. -
科目: 来源: 题型:
查看答案和解析>>【题目】多项式1﹣2x4y﹣3x3y2﹣y4+x2y3按y的降幂排列为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,反比例函数y=
 , 在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点.若四边形BEDF的面积为6,则k的值为( )
, 在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点.若四边形BEDF的面积为6,则k的值为( )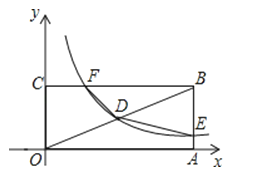
A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】比较大小:
-(-3.5)____﹣|-4.5|,38.15°_____ 38°15′(填“>”“<”或“=”).
相关试题

