【题目】已知抛物线![]() 与x轴相交于不同的两点
与x轴相交于不同的两点![]() ,
,
(1)求![]() 的取值范围
的取值范围
(2)证明该抛物线一定经过非坐标轴上的一点![]() ,并求出点
,并求出点![]() 的坐标;
的坐标;
(3)当![]() 时,由(2)求出的点
时,由(2)求出的点![]() 和点
和点![]() 构成的
构成的![]() 的面积是否有最值,若有,求出最值及相对应的
的面积是否有最值,若有,求出最值及相对应的![]() 值;若没有,请说明理由.
值;若没有,请说明理由.
参考答案:
【答案】(1)![]() 且
且![]() ;(2)(3,4);(3)详见解析.
;(2)(3,4);(3)详见解析.
【解析】
试题分析:(1)根据根的判别式求出m的取值范围,注意![]() ;(2)令
;(2)令![]() ,得出
,得出![]() ,故过定点P(3,4);(3)利用韦达定理写出AB的长度
,故过定点P(3,4);(3)利用韦达定理写出AB的长度![]() ,再根据m的取值范围,求出
,再根据m的取值范围,求出![]() 的面积的最大值.
的面积的最大值.
试题解析:(1)根据已知可知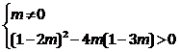
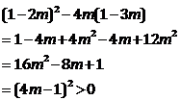
所以 ![]() 所以
所以![]()
所以m的取值范围为![]() 且
且![]() .
.
(2)令![]() ,则
,则![]() ,令
,令![]() 得
得![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;所以抛物线过定点(-1,0),(3,4),因为(-1,0)在x轴上,所以抛物线一定经过非坐标轴上一点P,P的坐标为(3,4)
;所以抛物线过定点(-1,0),(3,4),因为(-1,0)在x轴上,所以抛物线一定经过非坐标轴上一点P,P的坐标为(3,4)
(3)设A,B的坐标为![]() ,则
,则![]()
![]()
![]()
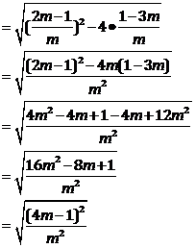
因为![]() ,所以
,所以![]() ,所以
,所以![]() =2AB
=2AB![]() =
=![]()
![]()
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,所以当
,所以当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() =
=![]()
考点:二次函数综合题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(c-a2b2)2 等于( )
A. c -ab2 B. c2 -2a2b2c+a4b4 C. c-a2b2c+a4b4 D. c2 -2abc+a4b
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数中,绝对值最大的数是( )
A. 5 B. ﹣3 C. 0 D. ﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件发生的概率为0的是( )
A. 随意掷一枚均匀的硬币两次,至少有一次反面朝上
B. 今年冬天黑龙江会下雪
C. 随意掷两个均匀的骰子,朝上面的点数之和为1
D. 一个转盘被分成6个扇形,按红、白、白、红、红、白排列,转动转盘,指针停在红色区域
-
科目: 来源: 题型:
查看答案和解析>>【题目】填写下面证明过程中的推理依据:
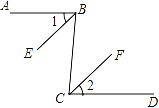
已知:如图,AB∥CD,BE平分∠ABC,CF平分∠BCD.求证:∠1=∠2
证明:∵AB∥CD ( )
∴∠ABC=∠BCD( )
∵BE平分∠ABC,CF平分∠BCD ( )
∴∠1=
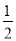 ∠ ABC ,( )
∠ ABC ,( )∠2=
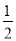 ∠ BCD . ( )
∠ BCD . ( )∴∠1=∠2. ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C为△ABD外接圆上的一动点(点C不在
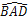 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.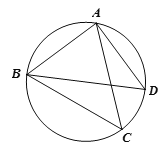
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:
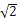 AC=BC+CD;
AC=BC+CD;(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究
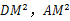 ,
,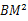 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】某银行办储蓄业务:取出950元,存入500元,取出800元,存入1200元,取出1025元,存入2500元,取出200元,请你计算一下,银行的现款增加了多少?
相关试题

