【题目】如图,有四张背面完全相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.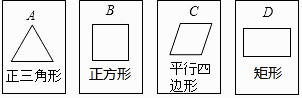
(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用A、B、C、D表示).
参考答案:
【答案】
(1)
解:共有4张牌,正面是中心对称图形的情况有3种,所以摸到正面是中心对称图形的纸牌的概率是 ![]() ;
;
(2)
解:列表得:
A | B | C | D | |
A | (A,B) | (A,C) | (A,D) | |
B | (B,A) | (B,C) | (B,D) | |
C | (C,A) | (C,B) | (C,D) | |
D | (D,A) | (D,B) | (D,C) |
共产生12种结果,每种结果出现的可能性相同,其中两张牌都是轴对称图形的有6种,
∴P(两张都是轴对称图形)= ![]() ,因此这个游戏公平.
,因此这个游戏公平.
【解析】(1)首先根据题意结合概率公式可得答案;(2)首先根据(1)求得摸出两张牌面图形都是轴对称图形的有16种情况,若摸出两张牌面图形都是中心对称图形的有12种情况,继而求得小明赢与小亮赢的概率,比较概率的大小,即可知这个游戏是否公平.
【考点精析】解答此题的关键在于理解轴对称图形的相关知识,掌握两个完全一样的图形关于某条直线对折,如果两边能够完全重合,我们就说这两个图形成轴对称,这条直线就对称轴,以及对列表法与树状图法的理解,了解当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一列火车匀速行驶,经过一条长300米的隧道需要20秒的时间.隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是10秒.求这列火车的长度.
小冉根据学习解决应用问题的经验对上面问题进行了探究,下面是小冉的探究过程,请补充完成:
设这列火车的长度是x米,那么
(1)从车头经过灯下到车尾经过灯下,火车所走的路程是 米,这段时间内火车的平均速度是 米/秒;
(2)从车头进入隧道到车尾离开隧道,火车所走的路程是 米,这段时间内火车的平均速度是 米/秒;
(3)火车经过灯下和火车通过隧道的平均速度的关系是 ;
(4)由此可以列出方程并求解出这列火车的长度(请列方程求解)
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(
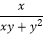 ﹣
﹣ 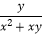 )÷(1﹣
)÷(1﹣ 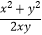 ),其中x=(
),其中x=(  )﹣1﹣(2017﹣
)﹣1﹣(2017﹣  )0 , y=
)0 , y= 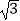 sin60°.
sin60°. -
科目: 来源: 题型:
查看答案和解析>>【题目】为打造徐州故黄河风光带,一段长为360米的河道整治任务交由甲、乙两个工程队接力完成,共用时20天.已知甲队每天整治24米,乙队每天整治16米.
(1)根据题意,小明、小丽分别列出如下的一元一次方程(尚不完整):
小明:24x+16 =360.
小丽:
 .
.请分别指出上述方程中x的意义,并补全方程:
小明:x表示: ;
小丽:x表示: .
(2)求甲、乙两队分别整治河道多少米?(写出完整的解答过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们,足球是世界上第一大运动,你热爱足球运动吗?已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一队共踢了30场比赛,负了9场,共得47分,那么这个队胜了( )
A. 10场 B. 11场 C. 12场 D. 13场
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
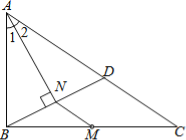
(1)求证:BN=DN;
(2)求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“*”是新规定的这样一种运算法则:a*b=a2+2ab,比如3*(﹣2)=32+2×3×(﹣2)=﹣3
(1)试求2*(﹣3)的值;
(2)若2*x=2,求x的值;
(3)若(﹣2)*(1*x)=x+9,求x的值.
相关试题

