【题目】如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的大小关系是;(填“>”或“<”或“=”) 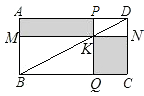
参考答案:
【答案】S1=S2 .
【解析】解:∵四边形ABCD是矩形,四边形MBQK是矩形,四边形PKND是矩形, ∴△ABD的面积=△CDB的面积,△MBK的面积=△QKB的面积,△PKD的面积=△NDK的面积,
∴△ABD的面积﹣△MBK的面积﹣△PKD的面积=△CDB的面积﹣△QKB的面积=△NDK的面积,
∴S1=S2 .
所以答案是S1=S2 .
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段MN平行于y轴,点M的坐标是(﹣1,3),若MN=4,则N的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(2x+1)(x﹣3)= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】植树节即将来临,学校组织七年级(2)班的同学去公园植树,规定男生每人植4棵,女生每人植3棵,李老师分给第一小组植40棵树的任务,已知该组有男生x人,女生y人,请列出关于x,y的二元一次方程:____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB的长为a,延长线段AB至点C,使BC=
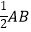 .
. 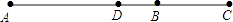
(1)求线段AC的长(用含a的代数式表示);
(2)取线段AC的中点D,若DB=3,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a2a3=a6
B.(﹣a3)2=﹣a6
C.(﹣3a2)2=6a4
D.(﹣a+b)(a+b)=b2﹣a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ∶S△ABC=9∶100?若存在,求出t的值;若不存在,说明理由;
(3)当t为何值时,△CPQ为等腰三角形?

相关试题

