【题目】数轴上点A对应的数为![]() ,点B对应的数为
,点B对应的数为![]() ,且多项式
,且多项式![]() 的二次项系数为
的二次项系数为![]() ,常数项为
,常数项为![]() .
.
(1)直接写出:![]() ;
;
(2)数轴上点A、B之间有一动点P,若点P对应的数为![]() ,试化简
,试化简![]() ;
;
(3)若点M从点A出发,以每秒1个单位长度的速度沿数轴向右移动;同时点N从点B出发,沿数轴每秒2个单位长度的速度向左移动,到达A点后立即返回并向右继续移动,求经过多少秒后,M、N两点相距1个单位长度?
参考答案:
【答案】(1)2,5;(2)x+8;(3)经过2秒或![]() 秒或7秒或8秒后,M、N两点相距1个单位长度.
秒或7秒或8秒后,M、N两点相距1个单位长度.
【解析】
(1)根据多项式的系数即可得出结论;
(2)先确定出x的范围,进而得出2x+4>0,x5<0,6x>0,最后去掉绝对值,合并即可得出结论;
(3)分点N未到达点A之前和之后,建立方程求解即可得出结论.
(1)∵多项式6x3y2xy+5的二次项系数为a,常数项为b,
∴a=2,b=5,
故答案为:2,5;
(2)∴数轴上点A对应的数为a,点B对应的数为b,
∴数轴上点A对应的数为2,点B对应的数为5,
∵数轴上点A、B之间有一动点P,点P对应的数为x,
∴2<x<5,
∴2x+4>0,x5<0,6x>0,
∴|2x+4|+2|x5||6x|=2x+42(x5)(6x)=2x+42x+106+x=x+8;
(3)设经过t秒后,M、N两点相距1个单位长度,
由运动知,AM=t,BN=2t,
①当点N到达点A之前时,
a、当M,N相遇前,M、N两点相距1个单位长度,
∴t+1+2t=5+2,
∴t=2秒,
b、当M,N相遇后,M、N两点相距1个单位长度,
∴t+2t1=5+2,
∴t=![]() 秒,
秒,
②当点N到达点A之后时,
a、当N未追上M时,M、N两点相距1个单位长度,
∴t[2t(5+2)]=1,
∴t=7秒;
b、当N追上M后时,M、N两点相距1个单位长度,
∴[2t(5+2)]t=1,
∴t=8秒;
即:经过2秒或![]() 秒或7秒或8秒后,M、N两点相距1个单位长度.
秒或7秒或8秒后,M、N两点相距1个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据要求完成下列题目:
(1)图中有 块小正方体;
(2)请在下面方格纸中分别画出它的主视图,左视图和俯视图.

(3)用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何体最少要 个小立方块,最多要 个小立方块.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:求值:1+2+22+23+24++22013.
解:设S=1+2+22+23+24+…+22013.将等式两边同时乘以2,得
2S=2+22+23+24+…+22013+22014
将下式减去上式,得2S﹣S=22014﹣1.
即S=1+2+22+23+24++22013=22014﹣1.
请你仿照此法计算1+3+32+33+34+…+32018的值是( )
A. 32018﹣1 B.
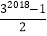 C. 32019﹣1 D.
C. 32019﹣1 D. 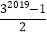
-
科目: 来源: 题型:
查看答案和解析>>【题目】某个体经营户销售同一型号的A、B两种品牌的服装,平均每月共销售60件,已知两种品牌的成本和利润如表所示,设平均每月的利润为y元,每月销售A品牌x件.
(1)写出y关于x的函数关系式.
(2)如果每月投入的成本不超过6500元,所获利润不少于2920元,不考虑其他因素,那么销售方案有哪几种?
(3)在(2)的条件下要使平均每月利润率最大,请直接写出A、B两种品牌的服装各销售多少件?A
B
成本(元/件)
120
85
利润(元/件)
60
30
-
科目: 来源: 题型:
查看答案和解析>>【题目】“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:

要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面文字,然后按要求解题.
例:1+2+3+…+100=?如果一个一个顺次相加显然太繁,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法的运算律,是可以大大简化计算,提高计算速度的.
因为1+100=2+99=3+98=…=50+51=101,所以将所给算式中各加数经过交换、结合以后,可以很快求出结果.
解:1+2+3+…+100=(1+100)+(2+99)+(3+98)+…+(50+51)=
 =5050.
=5050.(1)补全例题
 解题过程;
解题过程;(2)计算a+(a+b)+(a+2b)+(a+3b)+…+(a+99b).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c的象经过A(﹣1,0)、B(3,0)、N(2,3)三点,且与y轴交于点C.
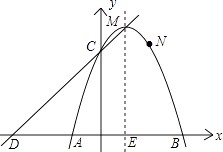
(1)求这个二次函数的解析式,并写出顶点M及点C的坐标;
(2)若直线y=kx+d经过C、M两点,且与x轴交于点D,试证明四边形CDAN是平行四边形;
(3)点P是这个二次函数的对称轴上一动点,请探索:是否存在这样的点P,使以点P为圆心的圆经过A、B两点,并且与直线CD相切?如果存在,请求出点P的坐标;如果不存在,请说明理由.
相关试题

