【题目】如图,等边△ABC的顶点A,B分别在函数y=-![]() 图象的两个分支上,且AB经过原点O.当点A在函数y=-
图象的两个分支上,且AB经过原点O.当点A在函数y=-![]() 的图象上移动时,顶点C始终在函数y=
的图象上移动时,顶点C始终在函数y=![]() 的图象上移动,则k的值为( )
的图象上移动,则k的值为( )

A. 8B. 6C. ![]() D. 2
D. 2
参考答案:
【答案】B
【解析】
根据反比例函数图象的对称性可得OA=OB,设OA=x,则AC=2x,OC=![]() x,根据等边三角形三线合一可证明△AOE∽△OCF,根据相似三角形面积比等于相似比的平方可得结论.
x,根据等边三角形三线合一可证明△AOE∽△OCF,根据相似三角形面积比等于相似比的平方可得结论.
解:∵函数y=-![]() 图象关于原点对称,
图象关于原点对称,
∴OA=OB,
连接OC,过A作AE⊥x轴于E,过C作CF⊥x轴于F,
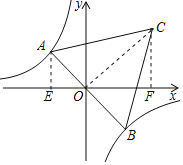
∵△ABC是等边三角形,
∴AO⊥OC,
∴∠AOC=90°,∠AOC=30°,
∴∠AOE+∠COF=90°,
设OA=x,则AC=2x,OC=![]() x,
x,
∵AE⊥x轴,CF⊥x轴,
∴∠AEO=∠OFC=∠AOE+∠OAE=90°,
∴∠COF=∠OAE,
∴△AOE∽△OCF,
∴![]() =
= =
= =
=![]() ,
,
∵顶点A在函数y=-![]() 图象的分支上,
图象的分支上,
∴S△AOE=1,
∴S△OCF=3,
∵顶点C始终在函数y=![]() 的图象上,
的图象上,
∴k=6,
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的中线BE,CD相交于点O,若△DOE的面积为1cm2,则△ABC的面积为( )

A. 12B. 8C. 6D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为矩形,E为BC边的中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.求证:CF与⊙O相切.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小红爸爸上星期五买进某公司股票1000股,每股28元,下表为本周内每日该股票的涨跌情况。(单位:元)
星期
一
二
三
四
五
每股涨跌
+4
+4.5
-1
-2.5
-6
(1)通过上表你认为星期三收盘时,每股是多少?
(2)本周内每股最高是多少?最低是多少元?
(3)已知小红爸爸买进股票时付了
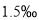 的手续费,卖出时还需付成交额,
的手续费,卖出时还需付成交额,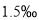 的手续费和
的手续费和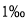 的交易税,如果小红爸爸在星期五收盘时将全部股票卖出,你对他的收益情况怎样评价?
的交易税,如果小红爸爸在星期五收盘时将全部股票卖出,你对他的收益情况怎样评价? -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程(组)及不等式(组)解应用题:
水是生命之源.为了鼓励市民节约用水,江夏区水务部门实行居民用水阶梯式计量水价政策;若居民每户每月用水量不超过10立方米,每立方米按现行居民生活用水水价收费(现行居民生活用水水价=基本水价+污水处理费);若每户每月用水量超过10立方米,则超过部分每立方米在基本水价基础上加价100%,但每立方米污水处理费不变.
下面表格是某居民小区4月份甲、乙两户居民生活用水量及缴纳生活用水水费的情况统计:
4月份居民用水情况统计表
(注:污水处理的立方数=实际生活用水的立方数)
用水量(立方米)
缴纳生活用水费用(元)
甲用户
8
27.6
乙用户
12
46.3
(1)求每立方米的基本水价和每立方米的污水处理费各是多少?
(2)设这个小区某居民用户5月份用水
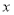 立方米,需要缴纳的生活用水水费为
立方米,需要缴纳的生活用水水费为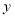 元.若他5月份生活用水水费计划不超过64元,该用户5月份最多可用水多少立方米?
元.若他5月份生活用水水费计划不超过64元,该用户5月份最多可用水多少立方米? -
科目: 来源: 题型:
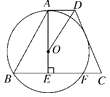
查看答案和解析>>【题目】如图,梯形ABCD中,AD∥BC,AE⊥BC于点E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B,交BC于另一点F.
(1)求证:CD与⊙O相切;
(2)若BF=24,OE=5,求tan∠ABC的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,交∠CBE的平分线于点N.
(1)写出点C的坐标;
(2)求证:MD=MN;
(3)连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,其中只有一个结论是正确的,请你指出正确的结论,并给出证明

相关试题

