【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为_____.

参考答案:
【答案】2![]() +2
+2
【解析】如图所示,
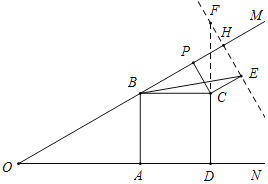
将BC绕着点C顺时针旋转90°得FC,作直线FE交OM于H,则∠BCF=90°,BC=FC,
∵将CP绕点C按顺时针方向旋转90°得CE,
∴∠PCE=90°,PC=EC,
∴∠BCP=∠FCE,
在△BCP和△FCE中,
BC=FC,∠BCP=∠FCE,PC=EC,
∴△BCP≌△FCE(SAS),
∴∠CBP=∠CFE,
又∵∠BCF=90°,
∴∠BHF=90°,
∴点E在直线FH上,即点E的轨迹为直线FH,
∵BH⊥EF,
∴当点E与点H重合时,BE=BH最短,
∵当CP⊥OM时,Rt△BCP中,∠CBP=30°,
∴CP=![]() BC=2,BP=
BC=2,BP=![]() CP=2
CP=2![]() ,
,
又∵∠PCE=∠CPH=∠PHE=90°,CP=CE,
∴正方形CPHE中,PH=CP=2,
∴BH=BH+PH=2![]() +2,
+2,
即BE的最小值为2![]() +2,
+2,
故答案为:2![]() +2.
+2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,那么阴影部分的面积是矩形ABCD面积的( )

A.
 B.
B.  C.
C.  D.
D. 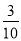
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2+bx+c经过点(3,0)和(4,0),则这个二次函数的解析式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知抛物线与直线的图象如图所示,当y1≠y2时,取y1,y2中的较大值记为N;当y1=y2时,N=y1=y2.则下列说法:①当0<x<2时,N=y1;②N随x的增大而增大的取值范围是x<0;③取y1,y2中的较小值记为M,则使得M大于4的x值不存在;④若N=2,则x=2﹣
 或x=1.其中正确的有( )
或x=1.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.xx2=x2
B.(xy)2=xy2
C.(x2)3=x6
D.x2+x2=x4 -
科目: 来源: 题型:
查看答案和解析>>【题目】把a3﹣2a2+a分解因式的结果是( )
A.a2(a﹣2)+a
B.a(a2﹣2a)
C.a(a+1)(a﹣1)
D.a(a﹣1)2 -
科目: 来源: 题型:
查看答案和解析>>【题目】2615个位上的数字是( )
A.2
B.4
C.6
D.8
相关试题

