【题目】如图,在平行四边形ABCD中,以点A为圆心,一定长为半径作圆弧,分别交AD、AB于点E、F;再分别以点E、F为圆心,大于 ![]() EF的长为半径作弧,两弧交于点G;作射线AG,交边CD于点H.若AB=6,AD=4,则四边形ABCH的周长与三角形ADH的周长之差为( )
EF的长为半径作弧,两弧交于点G;作射线AG,交边CD于点H.若AB=6,AD=4,则四边形ABCH的周长与三角形ADH的周长之差为( ) 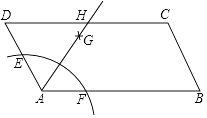
A.4
B.5
C.6
D.7
参考答案:
【答案】A
【解析】解:根据作图的方法可得AG平分∠DAB,
∵AG平分∠DAB,
∴∠DAH=∠BAH,
∵CD∥AB,
∴∠DHA=∠BAH,
∴∠DAH=∠DHA,
∴AD=DH,
∵AB=CD=6,AD=BC=4,
∴CH=6﹣4=2,
∴四边形ABCH的周长与三角形ADH的周长之差=(AB+BC+CH+AH)﹣(AD+AH+DH)=AB+CH﹣DH=6+2﹣4=4,
故选A.

【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上,以及对平行四边形的性质的理解,了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,则∠EBC等于( )
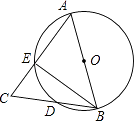
A.22.5°
B.23°
C.25°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,△A1B1C1是△ABC向右平移四个单位长度后得到的,且三个顶点的坐标分别为A1(1,1),B1(4,2),C1(3,4).

(1)请画出△ABC,并写出点A、B、C的坐标;
(2)求出△AOA1的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架梯子AC长2.5米,斜靠在一面墙上,梯子底端离墙0.7米.
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了0.4米到A′,那么梯子的底端在水平方向滑动了几米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板拼成如图所示的图形,即
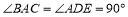 ,
, ,
, ,
,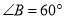 ,
,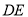 与
与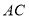 相交于点
相交于点 .
.

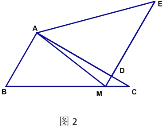
(1)如果
 ,那么
,那么 与
与 平行吗?试说明理由;
平行吗?试说明理由;(2)将
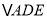 绕着点
绕着点 逆时针旋转,使得点
逆时针旋转,使得点 落在边
落在边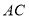 上,联结
上,联结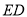 并延长交
并延长交 于点
于点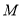 ,联结
,联结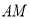 ,若
,若 ,
, ,
, ,求
,求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:(﹣2)﹣1﹣(2017﹣π)0+sin30°;
(2)化简: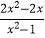 ﹣
﹣ 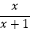 .
.
相关试题

