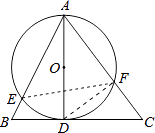
【题目】如图,在△ABC中,AC=BC,D是BC上的一点,且满足∠BAD= ![]() ∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
(1)求证:直线BC是⊙O的切线;
(2)连接EF,若tan∠AEF= ![]() ,AD=4,求BD的长.
,AD=4,求BD的长.
参考答案:
【答案】
(1)证明:在△ABC中,
∵AC=BC,
∴∠CAB=∠B,
∵∠CAB+∠B+∠C=180°,
∴2∠B+∠C=180°,
∴∠B+ ![]() ∠C=90°,
∠C=90°,
∵∠BAD= ![]() ∠C,
∠C,
∴∠B+∠BAD=90°,
∴∠ADB=90°,
∴AD⊥BC,
∵AD为⊙O直径,
∴直线BC是⊙O的切线;
(2)解:如图,连接DF,EF.
∵AD是⊙O的直径,
∴∠AFD=90°,
∵∠ADC=90°,
∴∠ADF+∠FDC=∠C+∠FDC=90°,
∴∠ADF=∠C,
∵∠ADF=∠AEF,tan∠AEF= ![]() ,
,
∴tan∠C=tan∠ADF= ![]() ,
,
在Rt△ACD中,设AD=4x,则CD=3x,
∴AC= ![]() =5x,
=5x,
∴BC=5x,BD=2x,
∵AD=4,
∴x=1,
∴BD=2.
【解析】(1)首先依据等腰三角形的性质得到∠CAB=∠B,然后结合三角形的内角和定理可得到∠B+ 1 2 ∠C=90°,然后依据题目条件可证明∠B+∠BAD=90°,然后依据切线的判定定理进行证明即可;
(2)连接DF,EF,由圆周角定理可知DF⊥AC,然后依据同角的余角相等得到∠ADF=∠C,接下来,依据同弧所对的圆周角相等得到∠ADF=∠AEF,由tan∠AEF的值得到tan∠ADF的值,设出AD=4x、DC=3x,再由AC=BC,根据BC-CD表示出BD,再由AD的长,最后,利用勾股定理求出x的值,从而可确定出BD的长.
【考点精析】根据题目的已知条件,利用勾股定理的概念和切线的判定定理的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如图所示,根据题中相关信息回答下列问题:
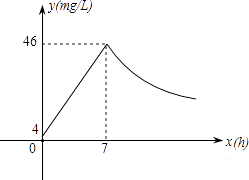
(1)求爆炸前后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;
(2)当空气中的CO浓度达到34mg/L时,井下3km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的CO浓度降到4mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c为三角形三边长,且方程b (x2-1)-2ax+c (x2+1)=0有两个相等的实数根. 试判断此三角形形状,说明理由.
-
科目: 来源: 题型:
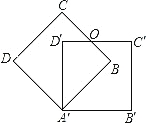
查看答案和解析>>【题目】把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( )
A. 6
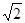 B. 6C. 3
B. 6C. 3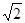 D. 3+3
D. 3+3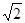
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论有( )

A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
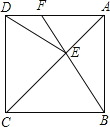
查看答案和解析>>【题目】如图,在一方形ABCD中.E为对角线AC上一点,连接EB、ED,
(1)求证:△BEC≌△DEC:
(2)延长BE交AD于点F,若∠DEB=140°.求∠AFE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某手机店今年1-4月的手机销售总额如图1,其中一款音乐手机的销售额占当月手机销售总额的百分比如图2.有以下四个结论:
①从1月到4月,手机销售总额连续下降
②从1月到4月,音乐手机销售额在当月手机销售总额中的占比连续下降
③音乐手机4月份的销售额比3月份有所下降
④今年1-4月中,音乐手机销售额最低的是3月
其中正确的结论是________(填写序号).

相关试题

