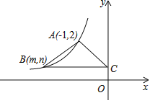
【题目】如图,在平面直角坐标系中,函数![]() (x<0,常数k<0)的图象经过点A(-1,2),B(m,n)且(m<-1),过点B作y轴的垂线,垂足为C,若△ABC面积为2,求点B的坐标.
(x<0,常数k<0)的图象经过点A(-1,2),B(m,n)且(m<-1),过点B作y轴的垂线,垂足为C,若△ABC面积为2,求点B的坐标.
参考答案:
【答案】点![]() 的坐标是
的坐标是![]() .
.
【解析】
由于函数y=![]() (x<0,常数k<0)的图象经过点A(-1,2),把(-1,2)代入解析式即可确定k=-2,依题意BC=-m,BC边上的高是2-n=2+
(x<0,常数k<0)的图象经过点A(-1,2),把(-1,2)代入解析式即可确定k=-2,依题意BC=-m,BC边上的高是2-n=2+![]() ,根据三角形的面积公式得到关于m的方程,解方程即可求出m,然后把m的值代入y=-
,根据三角形的面积公式得到关于m的方程,解方程即可求出m,然后把m的值代入y=-![]() ,即可求得B的纵坐标,最后就求出点B的坐标.
,即可求得B的纵坐标,最后就求出点B的坐标.
∵ 函数![]() ,(x<0,常数k<0)的图象经过点
,(x<0,常数k<0)的图象经过点![]() ,
,
∴ 把![]() 代入解析式得
代入解析式得![]() ,
,
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,当
,当![]() 时,
时,![]() ,
,
∴ ![]() 边上的高是
边上的高是![]() ,
,
而![]() ,
,
∴ ![]() ,
,
∴ 把![]() 代入
代入![]() ,
,
∴ ![]() ,
,
∴ 点![]() 的坐标是
的坐标是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:梯形ABCD中,AD//BC,AB⊥BC,AD=3,AB=6,DF⊥DC分别交射线AB、射线CB于点E、F.
(1)当点E为边AB的中点时(如图1),求BC的长;
(2)当点E在边AB上时(如图2),联结CE,试问:∠DCE的大小是否确定?若确定,请求出∠DCE的正切值;若不确定,则设AE=x,∠DCE的正切值为y,请求出y关于x的函数解析式,并写出定义域;
(3)当△AEF的面积为3时,求△DCE的面积.
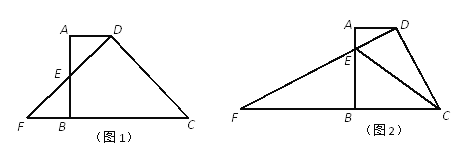
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20
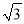 米.
米.(1)求出大厦的高度BD;
(2)求出小敏家的高度AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
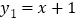 的图象与反比例函数
的图象与反比例函数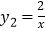 的图象交于
的图象交于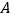 、
、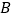 两点,过点
两点,过点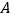 作
作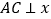 轴于点
轴于点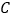 ,过点
,过点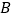 作
作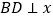 轴于点
轴于点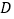 ,连接
,连接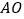 、
、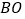 ,下列说法正确的是( )
,下列说法正确的是( )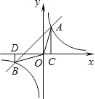
A. 点
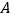 和点
和点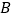 关于原点对称 B. 当
关于原点对称 B. 当 时,
时,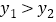
C.
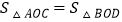 D. 当
D. 当 时,
时,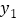 、
、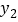 都随
都随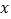 的增大而增大
的增大而增大 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=kx+b的图象与反比例函数
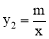 的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).
的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).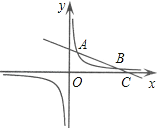
(1)求这两个函数的解析式;
(2)当x取何值时,y1>y2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角三角板
 放在平面直角坐标系中,直角边
放在平面直角坐标系中,直角边 垂直
垂直 轴,垂足为
轴,垂足为 ,已知
,已知 ,点
,点 ,
, ,
, 均在反比例函数
均在反比例函数 的图象上,分别作
的图象上,分别作 轴于
轴于 ,
, 轴于
轴于 ,延长
,延长 ,
, 交于点
交于点 ,且点
,且点 为
为 的中点.
的中点.
 求点
求点 的坐标;
的坐标; 求四边形
求四边形 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2
 cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

