【题目】如果多项式3x3﹣2x2+x+|k|x2﹣5中不含x2项,则k的值为( )
A.±2
B.﹣2
C.2
D.0
参考答案:
【答案】A
【解析】解:要使3x3﹣2x2+x+|k|x2﹣5中不含x2项,那么x2项的系数应为0,
在多项式3x3﹣2x2+x+|k|x2﹣5中﹣2x2和|k|x2两项含x2 ,
∴在合并同类项时这两项的系数互为相反数,结果为0,
即﹣2=﹣|k|,
∴k=±2.
故选A.
【考点精析】解答此题的关键在于理解多项式的相关知识,掌握几个单项式的和叫多项式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正多边形的每一个内角为135°,则该正多边形的边数为( )
A.12B.10C.8D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:ax2﹣4axy+4ay2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )

A.ac>0
B.当x>1时,y随x的增大而增大
C.2a+b=1
D.方程ax2+bx+c=0有一个根是x=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:a11÷a7=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P(m+1,m–1)在x轴上,则点P的坐标是( )
A.(2,0)B.(0,2)C.(–2,0)D.(0,–2)
-
科目: 来源: 题型:
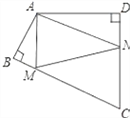
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为_______.
相关试题

