【题目】已知二次函数y=x2﹣2mx+4m﹣8
(1)当x≤2时,函数值y随x的增大而减小,求m的取值范围.
(2)以抛物线y=x2﹣2mx+4m﹣8的顶点A为一个顶点作该抛物线的内接正三角形AMN(M,N两点在拋物线上),请问:△AMN的面积是与m无关的定值吗?若是,请求出这个定值;若不是,请说明理由.
(3)若抛物线y=x2﹣2mx+4m﹣8与x轴交点的横坐标均为整数,求整数m的最小值.
参考答案:
【答案】
(1)解:二次函数y=x2﹣2mx+4m﹣8的对称轴是:x=m.
∵当x≤2时,函数值y随x的增大而减小,
而x≤2应在对称轴的左边,
∴m≥2.
(2)解:如图:
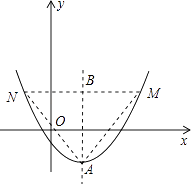
顶点A的坐标为(m,﹣m2+4m﹣8)
△AMN是抛物线的内接正三角形,
MN交对称轴于点B,tan∠AMB=tan60°= ![]() =
= ![]() ,
,
则AB= ![]() BM=
BM= ![]() BN,
BN,
设BM=BN=a,则AB= ![]() a,
a,
∴点M的坐标为(m+a, ![]() a﹣m2+4m﹣8),
a﹣m2+4m﹣8),
∵点M在抛物线上,
∴ ![]() a﹣m2+4m﹣8=(m+a)2﹣2m(m+a)+4m﹣8,
a﹣m2+4m﹣8=(m+a)2﹣2m(m+a)+4m﹣8,
整理得:a2﹣ ![]() a=0
a=0
得:a= ![]() (a=0舍去)
(a=0舍去)
所以△AMN是边长为2 ![]() 的正三角形,
的正三角形,
S△AMN= ![]() ×2
×2 ![]() ×3=3
×3=3 ![]() ,与m无关;
,与m无关;
(3)解:当y=0时,x2﹣2mx+4m﹣8=0,
解得:x=m± ![]() =m±
=m± ![]() ,
,
∵抛物线y=x2﹣2mx+4m﹣8与x轴交点的横坐标均为整数,
∴(m﹣2)2+4应是完全平方数,
∴m的最小值为:m=2.
【解析】(1)首先依据二次函数的对称轴公式求得抛物线的对称轴为x=m,由于a>0可得到抛物线的开口向上,故此在对称轴的左边y随x的增大而减小,从而可得到关于m的不等式;
(2)在抛物线内作出正三角形,顶点A的坐标为(m,﹣m2+4m﹣8),设BM=BN=a,则AB= ![]() a,故此可得到点M的坐标为(m+a, 3 a﹣m2+4m﹣8),然后将点M的坐标代入抛物线的解析式可求得a的值,从而得到等边三角形的边长,从而可求得△AMN的面积是m无关的定值;
a,故此可得到点M的坐标为(m+a, 3 a﹣m2+4m﹣8),然后将点M的坐标代入抛物线的解析式可求得a的值,从而得到等边三角形的边长,从而可求得△AMN的面积是m无关的定值;
(3)首先令y=0,从而可求出抛物线与x轴的两个交点的坐标,然后确定整数m的值即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°∠DAB=45°.(1)求∠DAC的度数;(2)请说明:AB=CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线AB∥DC,点P为平面上一点,连接AP与CP.
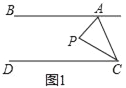
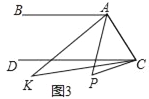
(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.
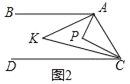
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D在AB边上,点D到点A的距离与点D到点C的距离相等.
(1)利用尺规作图作出点D,不写作法但保留作图痕迹.
(2)若△ABC的底边长5,周长为21,求△BCD的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:
已知:如图,
 ,
, ,
, ,求证:
,求证:

证明:∵
 ,
,
∴

∴
 ( )
( )又∵
 (已知)
(已知)∴
 ( )
( )∴
 ( )
( )∴
 ( )
( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】某书店老板去图书批发市场购买某种图书,第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书的数量比第一次多10本,当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.
(1)第一次购书的进价是多少元?
(2)试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其他因素)?若赔钱,赔多少;若赚钱,赚多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校男子足球队的年龄分布如条形图所示,则这些队员年龄的众数、中位数、平均数分别是( )
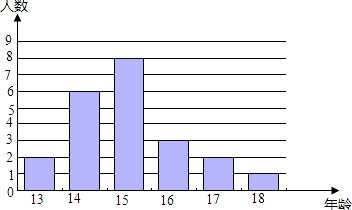
A.15、14、15
B.14、15、15
C.15、15、14
D.15、15、15
相关试题

