【题目】传统节日“端午节”的早晨,小文妈妈为小文准备了四个粽子作早点:一个枣馅粽,一个肉馅粽,两个花生馅粽,四个粽子除内部馅料不同外,其它一切均相同.
(1)小文吃前两个粽子刚好都是花生馅粽的概率为 ;
(2)若妈妈在早点中给小文再增加一个花生馅的粽子,则小文吃前两个粽子都是花生馅粽的可能性是否会增大?请说明理由.
参考答案:
【答案】(1)![]() ;(2)会增大.
;(2)会增大.
【解析】试题分析:(1)首先分别用A,B,C表示一个枣馅粽,一个肉馅粽,两个花生馅粽,然后根据题意画树状图,再由树状图求得所有等可能的结果与小文都是花生馅的情况,然后利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小文吃前两个都是花生的情况,再利用概率公式即可求得给小文再增加一个花生馅的粽子,比较大小即可.
试题解析:解:(1)分别用A,B,C表示一个枣馅粽,一个肉馅粽,两个花生馅粽,画树状图得:
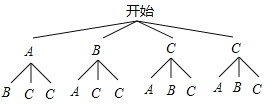
∵共有12种等可能的结果,小文吃前两个粽子刚好都是花生馅的有2种情况,∴小文吃前两个粽子刚好都是花生馅粽的概率: ![]() =
=![]() ,故答案为:
,故答案为: ![]() ;
;
(2)会增大,理由:分别用A,B,C表示一个枣馅粽,一个肉馅粽,三个花生馅粽,画树状图得:
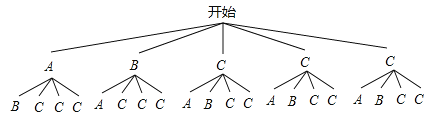
∵共有20种等可能的结果,两个都是花生的有6种情况,∴都是花生的概率为: ![]() =
=![]() >
>![]() ;
;
∴给小文再增加一个花生馅的粽子,则小文吃前两个粽子都是花生馅粽的可能性会增大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式2m2﹣4m4+2m﹣1按m的升幂排列_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把二元一次方程3x-y=1变形成用x的代数式表示y,则y=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC和△ADE均为等边三角形,连接BE,CD,点F,G,H分别为DE,BE,CD中点.
(1)当△ADE绕点A旋转时,如图1,则△FGH的形状为 ,说明理由;
(2)在△ADE旋转的过程中,当B,D,E三点共线时,如图2,若AB=3,AD=2,求线段FH的长;
(3)在△ADE旋转的过程中,若AB=a,AD=b(a>b>0),则△FGH的周长是否存在最大值和最小值,若存在,直接写出最大值和最小值;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程:

如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(______________ _________),
∴∠2 =∠CGD(等量代换).
∴CE∥BF(___________________ ________).
∴∠ =∠C(__________________________).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD(________________________________).
-
科目: 来源: 题型:
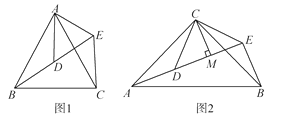
查看答案和解析>>【题目】(1)如图1,△ABC与△ADE均是顶角为40°的等腰三角形,BC,DE分别是底边,求证:BD=CE.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.
①求∠AEB的度数;
②证明:AE=BE+2CM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,CE,BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3……
第n次操作,分别作∠ABEn-1和∠DCEn-1的平分线,交点为En.

(1)如图①,求证:∠E=∠B+∠C;
(2)如图②,求证:∠E1=
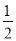 ∠E;
∠E;(3)猜想:若∠En=b°,求∠BEC的度数.
相关试题

