【题目】如图,△ABC与△CDE都是等边三角形,点E、F分别为AC、BC的中点。
(1) 求证:四边形EFCD是菱形;(2)如果AB=10,求D、F两点间的距离。

参考答案:
【答案】(1)证明见解析(2)![]()
【解析】
试题分析:(1)利用三角形的中位线定理即可得到四边形EFCD的四边相等,即可证得;
(2)连接DF,与EC相交于点G,△EFC是等边三角形,则△EFG是直角三角形,利用三角函数即可求得GF的长,根据DF=2GF即可求得.
试题解析:(1)∵△ABC与△CDE都是等边三角形
∴ AB=AC=BC,ED=DC=EC
∵ 点E、F分别为AC、BC的中点
∴EF= ![]() ,EC=
,EC= ![]() , FC=
, FC=![]()
∴EF=EC=FC
∴EF=FC=ED=DC,
∴四边形EFCD是菱形.
(2)连接DF,与EC相交于点G,
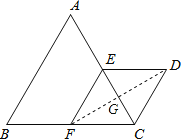
∵四边形EFCD是菱形
∴DF⊥EC,FD=2FG
∵EF= ![]() =5, EG=
=5, EG=![]() EC=
EC=![]() ,
,
由勾股定理得:FG=![]() ,则FD=
,则FD=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】设六边形的外角和等于a,五边形的内角和等于b,则a与b的关系是( )
A.a>b
B.b=a+180°
C.a<b
D.a=b -
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b,c为△ABC的三边长,且满足|a﹣5|+(b﹣3)2=0,则c的值可以为( )
A.7
B.8
C.9
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是外角和的3倍,则这个多边形是( )
A. 五边形 B. 六边形 C. 七边形 D. 八边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.
求证:BF=AE.

(2) 如图2,正方形ABCD边长为12,将正方形沿MN折叠,使点A落在DC边上的点E处,且DE=5,求折痕MN的长。

(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上,EF,GH交于点O,
∠FOH=90°,EF=4. 直接写出下列两题的答案:
①如图3,矩形ABCD由2个全等的正方形组成,则 GH=___________;
②如图4,矩形ABCD由n个全等的正方形组成,则 GH=___________;(用n的代数式表示).

-
科目: 来源: 题型:
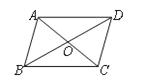
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.其中一定能判断这个四边形是平行四边形的条件共有( )
A.1组 B.2组 C.3组 D.4组
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=2是关于x的方程2x﹣3m﹣1=0的解,则m的值为__ .
相关试题

