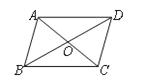
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.其中一定能判断这个四边形是平行四边形的条件共有( )
A.1组 B.2组 C.3组 D.4组
参考答案:
【答案】C
【解析】
试题分析:根据平行四边形的判断定理可作出判断:
①据平行四边形的判定定理:两组对边分别平行的四边形是平行四边形,可知①能判断这个四边形是平行四边形;
②根据平行四边形的判定定理:两组对边分别相等的四边形是平行四边形,可知②能判断这个四边形是平行四边形;
③根据平行四边形的判定定理:两条对角线互相平分的四边形是平行四边形,可知③能判断这个四边形是平行四边形;
④根据平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形,可知④不能判断这个四边形是平行四边形;
故给出下列四组条件中,①②③能判断这个四边形是平行四边形,
故选:C,
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是外角和的3倍,则这个多边形是( )
A. 五边形 B. 六边形 C. 七边形 D. 八边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC与△CDE都是等边三角形,点E、F分别为AC、BC的中点。
(1) 求证:四边形EFCD是菱形;(2)如果AB=10,求D、F两点间的距离。

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.
求证:BF=AE.

(2) 如图2,正方形ABCD边长为12,将正方形沿MN折叠,使点A落在DC边上的点E处,且DE=5,求折痕MN的长。

(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上,EF,GH交于点O,
∠FOH=90°,EF=4. 直接写出下列两题的答案:
①如图3,矩形ABCD由2个全等的正方形组成,则 GH=___________;
②如图4,矩形ABCD由n个全等的正方形组成,则 GH=___________;(用n的代数式表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=2是关于x的方程2x﹣3m﹣1=0的解,则m的值为__ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若单项式-3ab的次数是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2+4x﹣3中,当x=﹣1时,y的值是 .
相关试题

