【题目】如图,已知抛物线y= ![]() (x+2)(x﹣4)与x轴交于点A,B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(x+2)(x﹣4)与x轴交于点A,B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(1)求点A,B,C的坐标;
(2)设动点N(﹣2,n),求使MN+BN的值最小时n的值;
(3)P是抛物线上一点,请你探究:是否存在点P,使以P,A,B为顶点的三角形与△ABD相似(△PAB与△ABD不重合)?若存在,求出点P的坐标;若不存在,说明理由.
参考答案:
【答案】
(1)解:令y=0得x1=﹣2,x2=4,
∴点A(﹣2,0)、B(4,0)
令x=0得y=﹣ ![]() ,
,
∴点C(0,﹣ ![]() )
)
(2)解:将x=1代入抛物线的解析式得y=﹣ ![]()
∴点M的坐标为(1,﹣ ![]() )
)
∴点M关于直线x=﹣2的对称点M′的坐标为(﹣5, ![]() )
)
设直线M′B的解析式为y=kx+b
将点M′、B的坐标代入得: 
解得: 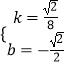
所以直线M′B的解析式为y= ![]() .
.
将x=﹣2代入得:y=﹣ ![]() ,
,
所以n=﹣ ![]() .
.
(3)解:过点D作DE⊥BA,垂足为E.
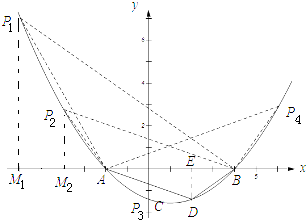
由勾股定理得:
AD= ![]() =3
=3 ![]() ,
,
BD= ![]() ,
,
如下图,①当P1AB∽△ADB时,
![]() 即:
即: ![]()
∴P1B=6 ![]()
过点P1作P1M1⊥AB,垂足为M1.
∴ ![]() 即:
即: ![]()
解得:P1M1=6 ![]() ,
,
∵ ![]() 即:
即: ![]()
解得:BM1=12
∴点P1的坐标为(﹣8,6 ![]() )
)
∵点P1不在抛物线上,所以此种情况不存在;
②当△P2AB∽△BDA时, ![]() 即:
即: ![]()
∴P2B=6 ![]()
过点P2作P2M2⊥AB,垂足为M2.
∴ ![]() ,即:
,即: ![]()
∴P2M2=2 ![]()
∵ ![]() ,即:
,即: ![]()
∴M2B=8
∴点P2的坐标为(﹣4,2 ![]() )
)
将x=﹣4代入抛物线的解析式得:y=2 ![]() ,
,
∴点P2在抛物线上.
由抛物线的对称性可知:点P2与点P4关于直线x=1对称,
∴P4的坐标为(6,2 ![]() ),
),
当点P3位于点C处时,两三角形全等,所以点P3的坐标为(0,﹣ ![]() ),
),
综上所述点P的坐标为:(﹣4,2 ![]() )或(6,2
)或(6,2 ![]() )或(0,﹣
)或(0,﹣ ![]() )时,以P、A、B为顶点的三角形与△ABD相似
)时,以P、A、B为顶点的三角形与△ABD相似
【解析】(1)令y=0可求得点A、B的横坐标,令x=0可求得C点的横坐标;(2)根据两点之间线段最短作M点关于直线X=-2的对称点M′,当点N在直线M′B上时MN+BN的值最小;(3)需要分类讨论;①当P1AB∽△ADB时,当△P2AB∽△BDA时根据相似三角形的性质求得PB的长度,然后求出P点的坐标。
【考点精析】本题主要考查了轴对称-最短路线问题和相似三角形的判定与性质的相关知识点,需要掌握已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题

(1)操作发现:
如图①,在正方形ABCD中,过A点有直线AP,点B关于AP的对称点为E,连接DE交AP于点F,当∠BAP=20°时,则∠AFD=°;当∠BAP=α°(0<α<45°)时,则∠AFD=;猜想线段DF,EF,AF之间的数量关系:DF﹣EF=AF(填系数);
(2)数学思考:
如图②,若将“正方形ABCD中”改成“菱形ABCD中,∠BAD=120°”,其他条件不变,则∠AFD=;线段DF,EF,AF之间的数量关系是否发生改变,若发生改变,请写出数量关系并说明理由;
(3)类比探究:
如图③,若将“正方形ABCD中”改成“菱形ABCD中,∠BAD=α°”,其他条件不变,则∠AFD=°;请直接写出线段DF,EF,AF之间的数量关系: . -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读理解:

如图①,在△ABC中,若AB=8,AC=4,求BC边上的中线AD的取值范围是
(2)问题解决:如图②,在△ABC中D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】每年的
 月
月 日为世界环保日,为了提倡低碳环保,某公司决定购买
日为世界环保日,为了提倡低碳环保,某公司决定购买 台节省能源的新设备,现有甲乙两种型号的设备可供选购,经调查:购买
台节省能源的新设备,现有甲乙两种型号的设备可供选购,经调查:购买 台甲型设备比购买
台甲型设备比购买 台乙型设备多花
台乙型设备多花 万元,购买
万元,购买 台甲型设备比购买
台甲型设备比购买 台乙型设备少花
台乙型设备少花 万元.
万元.(1)求甲乙两种型号设备的价格;
(2)该公司决定购买甲型设备不少于
 台,预算购买节省能源的新设备的资金不超过
台,预算购买节省能源的新设备的资金不超过 万元,你认为该公司有那几种购买方案?
万元,你认为该公司有那几种购买方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于( )

A.75
B.100
C.120
D.125 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,BE平分∠ABC,点P在射线BE上.

(1)如图1,若∠ABC=40°,CP∥AB,求∠BPC的度数;
(2)如图2,若∠BAC=100°,∠PBC=∠PCA,求∠BPC的度数;
(3)若∠ABC=40°,∠ACB=30°,直线CP与△ABC的一条边垂直,画出相应图形并求∠BPC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.
如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B;…
设游戏者从圈A起跳.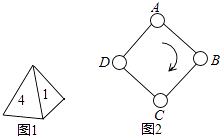
(1)嘉嘉随机掷一次骰子,求落回到圈A的概率P1;
(2)淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2 , 并指出她与嘉嘉落回到圈A的可能性一样吗?
相关试题

