【题目】如图所示,图1是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个全等的小长方形,再按图2围成一个较大的正方形. 
(1)请用两种方法表示图2中阴影部分的面积(只需表示,不必化简);
(2)比较(1)的两种结果,你能得到怎样的等量关系?
(3)请你用(2)中得到的等量关系解决下面问题:如果m﹣n=4,mn=12,求m+n的值.
参考答案:
【答案】
(1)解:方法一:∵大正方形的面积为(m+n)2,四个小长方形的面积为4mn,
∴中间阴影部分的面积为S=(m+n)2﹣4mn.
方法二:∵中间小正方形的边长为m﹣n,∴其面积为(m﹣n)2.
(2)解:(m+n)2﹣4mn=(m﹣n)2或(m+n)2=(m﹣n)2+4mn).
(3)解:由(2)得(m+n)2﹣4×12=42,即(m+n)2=64,
∴m+n=±8.又m、n非负,∴m+n=8.
【解析】(1)观察图形可确定:方法一,大正方形的面积为(m+n)2 , 四个小长方形的面积为4mn,中间阴影部分的面积为S=(m+n)2﹣4mn;方法二,图2中阴影部分为正方形,其边长为m﹣n,所以其面积为(m﹣n)2 . (2)观察图形可确定,大正方形的面积减去四个小长方形的面积等于中间阴影部分的面积,即(m+n)2﹣4mn=(m﹣n)2或(m+n)2=(m﹣n)2+4mn.(3)由(2)得,将m﹣n=4,mn=12,代入(2)式可求m+n=8.
【考点精析】利用完全平方公式对题目进行判断即可得到答案,需要熟知首平方又末平方,二倍首末在中央.和的平方加再加,先减后加差平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正比例函数y=kx的y值随x的增大而减小,则此函数的图象经过( )
A. 一、二象限 B. 一、三象限 C. 二、三象限 D. 二、四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料: 解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解:∵x﹣y=2,又∵x>1,∴y+2>1,即y>﹣1
又y<0,∴﹣1<y<0.…①
同理得:1<x<2.…②
由①+②得﹣1+1<y+x<0+2,∴x+y的取值范围是0<x+y<2.
请按照上述方法,完成下列问题:
已知关于x、y的方程组 的解都为非负数.
的解都为非负数.
(1)求a的取值范围;
(2)已知2a﹣b=1,且,求a+b的取值范围;
(3)已知a﹣b=m(m是大于1的常数),且b≤1,求2a+b最大值.(用含m的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BP=BQ,连结CQ.
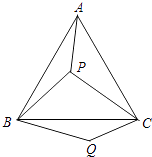
(1)观察并猜想AP与CQ之间的大小关系,并说明理由.
(2)若PA=3,PB=4,PC=5,连结PQ,判断△PQC的形状并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2a2+ab= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,欲用一块面积为800cm2的等腰梯形彩纸作风筝,用竹条作梯形的对角线且对角线恰好互相垂直,那么需要竹条多少厘米?
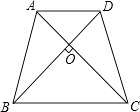
相关试题

