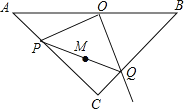
【题目】如图,等腰Rt△ABC中,斜边AB的长为2,O为AB的中点,P为AC边上的动点,OQ⊥OP交BC于点Q,M为PQ的中点,当点P从点A运动到点C时,点M所经过的路线长为( )
A. ![]() B.
B. ![]() C. 1 D. 2
C. 1 D. 2
参考答案:
【答案】C
【解析】连接OC,作PE⊥AB于E,MH⊥AB于H,QF⊥AB于F,如图,利用等腰直角三角形的性质得AC=BC=![]() ,∠A=∠B=45°,OC⊥AB,OC=OA=OB=1,∠OCB=45°,再证明Rt△AOP≌△COQ得到AP=CQ,接着利用△APE和△BFQ都为等腰直角三角形得到PE=
,∠A=∠B=45°,OC⊥AB,OC=OA=OB=1,∠OCB=45°,再证明Rt△AOP≌△COQ得到AP=CQ,接着利用△APE和△BFQ都为等腰直角三角形得到PE=![]() AP=
AP=![]() CQ,QF=
CQ,QF=![]() BQ,所以PE+QF=
BQ,所以PE+QF=![]() BC=1,然后证明MH为梯形PEFQ的中位线得到MH=
BC=1,然后证明MH为梯形PEFQ的中位线得到MH=![]() ,即可判定点M到AB的距离为
,即可判定点M到AB的距离为![]() ,从而得到点M的运动路线为△ABC的中位线,最后利用三角形中位线性质得到点M所经过的路线长.
,从而得到点M的运动路线为△ABC的中位线,最后利用三角形中位线性质得到点M所经过的路线长.
连接OC,作PE⊥AB于E,MH⊥AB于H,QF⊥AB于F,如图,
∵△ACB为到等腰直角三角形,
∴AC=BC=![]() AB=
AB=![]() ,∠A=∠B=45°,
,∠A=∠B=45°,
∵O为AB的中点,
∴OC⊥AB,OC平分∠ACB,OC=OA=OB=1,
∴∠OCB=45°,
∵∠POQ=90°,∠COA=90°,
∴∠AOP=∠COQ,
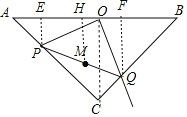
在Rt△AOP和△COQ中
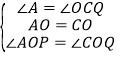 ,
,
∴Rt△AOP≌△COQ,
∴AP=CQ,
易得△APE和△BFQ都为等腰直角三角形,
∴PE=![]() AP=
AP=![]() CQ,QF=
CQ,QF=![]() BQ,
BQ,
∴PE+QF=![]() (CQ+BQ)=
(CQ+BQ)=![]() BC=
BC=![]() =1,
=1,
∵M点为PQ的中点,
∴MH为梯形PEFQ的中位线,
∴MH=![]() (PE+QF)=
(PE+QF)=![]() ,
,
即点M到AB的距离为![]() ,
,
而CO=1,
∴点M的运动路线为△ABC的中位线,
∴当点P从点A运动到点C时,点M所经过的路线长=![]() AB=1,
AB=1,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学分别进行6次射击训练,训练成绩(单位:环)如下表
第一次
第二次
第三次
第四次
第五次
第六交
甲
9
8
6
7
8
10
乙
8
7
9
7
8
8
对他们的训练成绩作如下分析,其中说法正确的是( )
A. 他们训练成绩的平均数相同 B. 他们训练成绩的中位数不同
C. 他们训练成绩的众数不同 D. 他们训练成绩的方差不同
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I'的坐标为( )
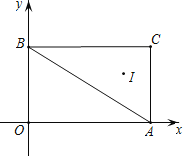
A. (﹣2,3) B. (﹣3,2) C. (3,﹣2) D. (2,﹣3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年端午节,在大明湖举行第七届会民健身运动会龙舟赛中,甲、乙两队在500米的赛道上,所划行的路程y(m)时间x(min)之间的关系如图所示,下列说法中正确的有( )
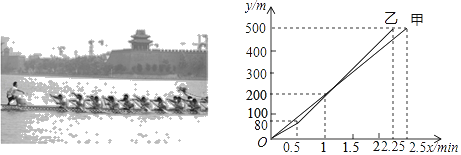
①乙队比甲队提前0.25min到达终点
②当乙队划行110m时,仍在甲队后面;
③当乙队划行200m时,已经超过甲队
④0.5min后,乙队比甲队每分钟快40m
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC交BC于点D,点M,N分别是AD和AB上的动点,当S△ABC=12,AC=8时,BM+MN的最小值等于_____.
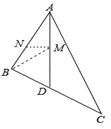
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,

(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P,使PA+PC最小,写出作法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB<AD,∠D=30°,CD=4,以AB为直径的⊙O交BC于点E,则阴影部分的面积为_____.
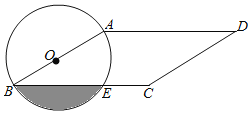
相关试题

