【题目】 在学习了全等三角形和等边三角形的知识后,张老师出了如下一道题:如图,点B是线段AC上任意一点,分别以AB、BC为边在AC同一侧作等边△ABD和等边△BCE,连接CD、AE分别与BE和DB交于点N、M,连接MN.
(1)求证:△ABE≌△DBC.

接着张老师又让学生分小组进行探究:你还能得出什么结论?
精英小组探究的结论是:AM=DN.
奋斗小组探究的结论是:△EMB≌△CNB.
创新小组探究的结论是:MN∥AC.
(2)你认为哪一小组探究的结论是正确的?
(3)选择其中你认为正确的一种情形加以证明.
参考答案:
【答案】(1)证明见解析;(2)三个小组探究的结论都正确;(3)证明见解析
【解析】试题分析:
(1)由△ABD和△BCE都是等边三角形可得:AB=DB,BC=BE,∠ABD=∠EBC=60°,这样可得∠ABE=∠DBC,从而可由“SAS”证得△ABE≌△DBC;
(2)由△ABE≌△DBC可得∠EAB=∠CDB,而由已知条件易证∠DBN=∠ABD=60°,结合AB=DB可证△ABM≌△DBN,就可得AM=DN;同理可证△EBM≌△CBN;由△EBM≌△CBN可得BM=BN,结合∠DBN=60°可得△BMN是等边三角形,从而可得∠MNB=60°=∠EBC,由此可得MN∥AC;故三个小组的探究结论都是正确的;
(3)根据(2)中的分析选择第一个结论证明即可;
试题解析:
(1∵△ABD和△BCE都是等边三角形,
∴AB=DB,BE=BC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC=120°,
∵在△ABE和△DBC中,AB=DB,∠ABE=∠DBC,BE=BC,
∴△ABE≌△DBC;
(2)三个小组探究的结论都正确;
(3)选择证明:AM=DN,过程如下:
∵△ABE≌△DBC,
∴∠EAB=∠CDB,
∵∠ABD+∠DBE+∠EBC=180°,∠ABD=∠EBC=60°,
∴∠DBE=∠ABD=60°,
∵在△ABM和△DBN中,∠MAB=∠NDB,AB=DB,∠DBN=∠ABM,
∴△ABM≌△DBN,
∴AM=DN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算,计算结果是错误的是( )
A.a4·a3=a7B.a6÷a3=a3C.(a3)2=a5D.a3·b3=(a·b)3
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣52的结果是;(﹣5)2的结果是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个数的商为正数,则两个数( )
A.都为正
B.都为负
C.同号
D.异号 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一种植物种子的质量约为0.0000026千克,将数0.0000026用科学记数法表示为( )
A. 2.6×10﹣6 B. 2.6×10﹣5 C. 26×10﹣8 D. 0.26x10﹣7
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题共10分)AB和AC 相交于点A, BD和CD相交于点D,探究∠BDC与∠B 、 ∠C、∠BAC的关系.
小明是这样做的:
解:以点A为端点作射线AD.
∵∠1是△ABD的外角,∴∠1= ∠B+∠BAD.
同理∠2=∠C+∠CAD.
∴∠1+∠2=∠B+∠BAD+∠C+∠CAD.即∠BDC=∠B+∠C+∠BAC.
小英的思路是:延长BD交AC于点E.
(1)按小英的思路完成∠BDC=∠B+∠C+∠BAC这一结论.



(2)按照上面的思路解决如下问题:如图:在△ABC中,BE、CD分别是∠ABC∠ACB的角平分线,交AC于E,交AB于D.BE、CD相交于点O,∠A=60°.求∠BOC的度数.

(3)如图:△ABC中,BO、CO分别是∠ABC与∠ACB的角平分线,且BO、CO相交于点O.猜想∠BOC与∠A有怎样的关系,并加以证明.
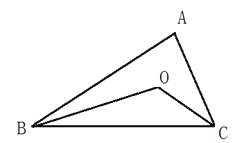
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
 的图象与性质.
的图象与性质.小东根据学习函数的经验,对函数
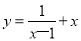 的图象与性质进行了探究.
的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
(1) 函数
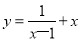 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;(2)下表是y与x的几组对应值.
x
…
-3
-2
-1
0




2
3
4
5
…
y
…






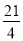

3

m

…
求m的值;
(3) 如图,在平面直角坐标系
 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可):
相关试题

