搜索
【题目】古希腊数学家把数1，3，6，10，15，21，…叫做三角形数，它有一定的规律性，若把第一个三角形数记为x1 ， 第二个三角形数记为x2 ， …第n个三角形数记为xn ， 则xn+xn+1= ．
参考答案：
【答案】（n+1）2
【解析】解：∵x1=1，
x2═3=1+2，
x3=6=1+2+3，
x4═10=1+2+3+4，
x5═15=1+2+3+4+5，
…
∴xn=1+2+3+…+n= 
，xn+1= 
，
则xn+xn+1= + =（n+1）2 ，
故答案为：（n+1）2 ．
根据三角形数得到x1=1，x2=3=1+2，x3=6=1+2+3，x4=10=1+2+3+4，x5=15=1+2+3+4+5，即三角形数为从1到它的顺号数之间所有整数的和，即xn=1+2+3+…+n= 、xn+1= ，然后计算xn+xn+1可得．
-
科目： 来源： 题型：
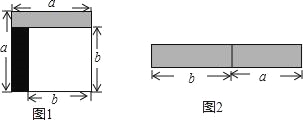
查看答案和解析>>【题目】从边长为a的正方形中剪掉一个边长为b的正方形（如图1），然后将剩余部分拼成一个长方形（如图2）．
（1）上述操作能验证的等式是 ；（请选择正确的一个）
A、a2﹣2ab+b2=（a﹣b）2
B、a2﹣b2=（a+b）（a﹣b）
C、a2+ab=a（a+b）
（2）应用你从（1）选出的等式，完成下列各题：
①已知x2﹣4y2=12，x+2y=4，求x﹣2y的值．
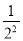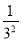②计算：（1﹣
）（1﹣
）（1﹣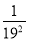
）…（1﹣
）（1﹣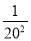
）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】班委会决定，选购圆珠笔、钢笔共22支，送给山区学校的同学。已知圆珠笔每支5元，钢笔每支6元。
（1）若购买圆珠笔、钢笔刚好用去120元，问圆珠笔、钢笔各买了多少支？
（2）若购圆珠笔可9折优惠，钢笔可8折优惠，在所需费用不超过100元的前提下，请你写出一种选购方案。
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知直线l1:y=x+n-2与直线l2:y=mx+n相交于点P(1,2).
(1)求m,n的值;
(2)请结合图象直接写出不等式mx+n>x+n-2的解集.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一次函数的图象过M(1,3),N(-2,12)两点.
(1)求函数的解析式;
(2)试判断点P(2a,-6a+8)是否在函数的图象上,并说明理由.
-
科目： 来源： 题型：
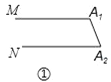
查看答案和解析>>【题目】下列各图中的MA1与NAn平行．
（1）图①中的∠A1+∠A2=______度，
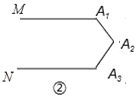
图②中的∠A1+∠A2+∠A3=______度，
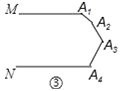
图③中的∠A1+∠A2+∠A3+∠A4=______度，
第⑩个图中的∠A1+∠A2+∠A3+…+∠A10=______度
（2）第n个图中的∠A1+∠A2+∠A3+…+∠An=______．
（3）证明图②中的结论.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某蔬菜加工公司先后两批次收购蒜薹(tái)共100吨．第一批蒜薹价格为4000元/吨；因蒜薹大量上市，第二批价格跌至1000元/吨．这两批蒜薹共用去16万元．
(1)求两批次购进蒜薹各多少吨；
(2)公司收购后对蒜薹进行加工，分为粗加工和精加工两种：粗加工每吨利润400元，精加工每吨利润1000元．要求精加工数量不多于粗加工数量的三倍．为获得最大利润，精加工数量应为多少吨？最大利润是多少？
相关试题
