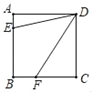
【题目】如图,正方形ABCD的边长为6,点E,F分别在边AB,BC上,若F是BC的中点,且∠EDF=45°,则DE的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
延长F至G,使CG=AE,连接DG,由SAS证明△ADE≌△CDG,得出DE=DG,∠ADE=∠CDG,再证明△EDF≌△GDF,得出EF=GF,设AE=CG=x,则EF=GF=3+x,在Rt△BEF中,由勾股定理得出方程,解方程得出AE=2,在Rt△ADE中,由勾股定理求出DE即可.
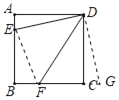
解:延长F至G,使CG=AE,连接DG、EF,如图所示:
∵四边形ABCD是正方形,
∴AD=AB=BC=CD=6,∠A=∠B=∠DCF=∠ADC=90°,
∴∠DCG=90°,
在△ADE和△CDG中,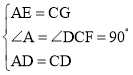 ,
,
∴△ADE≌△CDG(SAS),
∴DE=DG,∠ADE=∠CDG,
∴∠EDG=∠CDE+∠CDG=∠CDE+∠ADE=90°,
∵∠EDF=45°,
∴∠GDF=45°,
在△EDF和△GDF中,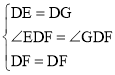 ,
,
∴△EDF≌△GDF(SAS),
∴EF=GF,
∵F是BC的中点,
∴BF=CF=3,
设AE=CG=x,则EF=GF=3+x,
在Rt△BEF中,由勾股定理得:32+(6﹣x)2=(3+x)2,
解得:x=2,即AE=2,
在Rt△ADE中,由勾股定理得:DE=![]() ;
;
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 某单位在二月份准备组织部分员工到北京旅游,现联系了甲、乙两家旅行社,两家旅行社报价均为2000元/人,两家旅行社同时都对10人以上的团体推出了优惠举措:甲旅行社对每位员工七五折优惠;而乙旅行社是免去一位带队管理员工的费用,其余员工八折优惠.
(1)如果设参加旅游的员工共有a(a
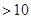 )人,则甲旅行社的费用为 元,乙旅行社的费用为 元;(用含a的代数式表示,并化简.)
)人,则甲旅行社的费用为 元,乙旅行社的费用为 元;(用含a的代数式表示,并化简.)(2)假如这个单位现组织包括管理员工在内的共20名员工到北京旅游,该单位选择哪一家旅行社比较优惠?请说明理由;
(3)如果计划在二月份外出旅游七天,设最中间一天的日期为m.
①这七天的日期之和为 ;(用含m的代数式表示,并化简.)
②假如这七天的日期之和为63的倍数,则他们可能于二月几号出发?(写出所有符合条件的可能性,并写出简单的计算过程.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】检修小组从A地出发,在东西路上检修线路,若规定向东行驶的路程为正数,向西行驶的路程为负数,一天中行驶记录(单位;千米)如下:
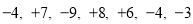
(1)收工时检修小组在A地的哪侧,距A地多远?
(2)若每千米耗油0.3升,从出发到收工共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是边长为
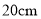 的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).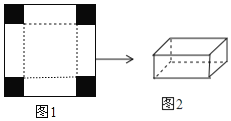
(1)设剪去的小正方形的边长为
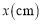 ,折成的长方体盒子的容积为
,折成的长方体盒子的容积为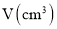 , 用只含字母
, 用只含字母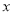 的式子表示这个盒子的高为________
的式子表示这个盒子的高为________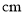 ,底面积为________
,底面积为________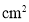 ,盒子的容积
,盒子的容积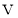 为________
为________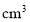 ;
;(2)为探究盒子的体积与剪去的小正方形的边长
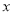 之间的关系,小明列表
之间的关系,小明列表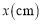
1
2
3
4
5
6
7
8
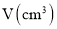
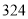
_______
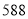
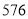
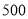
_______
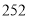
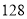
请将表中数据补充完整,并根据表格中的数据写出当
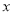 的值逐渐增大时,
的值逐渐增大时,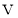 的值如何变化?
的值如何变化? -
科目: 来源: 题型:
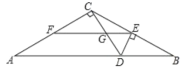
查看答案和解析>>【题目】如图,已知EF是△ABC的中位线,DE⊥BC交AB于点D,CD与EF交于点G,若CD⊥AC,EF=8,EG=3,则AC的长为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,边长为a的正方形发生形变后成为边长为a的菱形,如果这个菱形的一组对边之间的距离为h,我们把
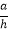 的值叫做这个菱形的“形变度”.例如,当形变后的菱形是如图2形状(被对角线BD分成2个等边三角形),则这个菱形的“形变度”为2:
的值叫做这个菱形的“形变度”.例如,当形变后的菱形是如图2形状(被对角线BD分成2个等边三角形),则这个菱形的“形变度”为2: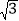 .如图3,正方形由16个边长为1的小正方形组成,形变后成为菱形,△AEF(A、E、F是格点)同时形变为△A′E′F′,若这个菱形的“形变度”k=
.如图3,正方形由16个边长为1的小正方形组成,形变后成为菱形,△AEF(A、E、F是格点)同时形变为△A′E′F′,若这个菱形的“形变度”k=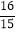 ,则S△A′E′F′=__
,则S△A′E′F′=__
-
科目: 来源: 题型:
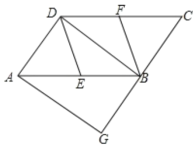
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、 F分别为边AB、CD的中点,BD是对角线.过点有作AG∥DB交CB的延长线于点G.
(1)求证:△ADE≌△CBF;
(2)若∠G=90° ,求证:四边形DEBF是菱形.
相关试题

