【题目】如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( ) 
A.y= ![]()
B.y= ![]()
C.y=2 ![]()
D.y=3 ![]()
参考答案:
【答案】B
【解析】解:∵ON是Rt∠AOB的平分线, ∴∠DOC=∠EOC=45°,
∵DE⊥OC,
∴∠ODC=∠OEC=45°,
∴CD=CE=OC=x,
∴DF=EF,DE=CD+CE=2x,
∵∠DFE=∠GFH=120°,
∴∠CEF=30°,
∴CF=CEtan30°= ![]() x,
x,
∴EF=2CF= ![]() x,
x,
∴S△DEF= ![]() DECF=
DECF= ![]() x2 ,
x2 ,
∵四边形FGMH是菱形,
∴FG=MG=FE= ![]() x,
x,
∵∠G=180°﹣∠GFH=60°,
∴△FMG是等边三角形,
∴S△FGH= ![]() x2 ,
x2 ,
∴S菱形FGMH= ![]() x2 ,
x2 ,
∴S阴影=S△DEF+S菱形FGMH= ![]() x2 .
x2 .
故选B.
【考点精析】根据题目的已知条件,利用菱形的性质和解直角三角形的相关知识可以得到问题的答案,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图正方形ABCD的边长为4,E、F分别为DC、BC中点.
(1)求证:△ADE≌△ABF.
(2)求△AEF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,梯形ABCD中,AB∥DC,∠B=90°,AD=15,AB=16,BC=12,点E是边AB上的动点,点F是射线CD上一点,射线ED和射线AF交于点G,且∠AGE=∠DAB.
(1)求线段CD的长;
(2)如果△AEC是以EG为腰的等腰三角形,求线段AE的长;
(3)如果点F在边CD上(不与点C、D重合),设AE=x,DF=y,求y关于x的函数解析式,并写出x的取值范围.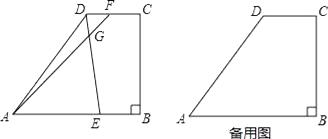
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线 y=ax2+bx+c(a≠0)经过点A(-3,0)、B(1,0)、C(-2,1),交y轴于点M.
(1)求抛物线的表达式;
(2)D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求此时点D的坐标;
(3)抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点P、A.N为顶点的三角形与△MAO相似?若存在,求点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图甲是小明设计的带菱形图案的花边作品.该作品由形如图乙的矩形图案拼接而成(不重叠、无缝隙).图乙中
 ,EF=4cm,上下两个阴影三角形的面积之和为54cm2 , 其内部菱形由两组距离相等的平行线交叉得到,则该菱形的周长为cm.
,EF=4cm,上下两个阴影三角形的面积之和为54cm2 , 其内部菱形由两组距离相等的平行线交叉得到,则该菱形的周长为cm. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔试
面试
体能
甲
83
79
90
乙
85
80
75
丙
80
90
73
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分.根据规定,请你说明谁将被录用. -
科目: 来源: 题型:
查看答案和解析>>【题目】各顶点都在方格纸格点(横竖格子线的交错点)上的多边形称为格点多边形.如何计算它的面积?奥地利数学家皮克(GPick,1859~1942年)证明了格点多边形的面积公式S=a+
 b﹣1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.如图,a=4,b=6,S=4+
b﹣1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.如图,a=4,b=6,S=4+  ×6﹣1=6
×6﹣1=6
(1)请在图中画一个格点正方形,使它的内部只含有4个格点,并写出它的面积.
(2)请在图乙中画一个格点三角形,使它的面积为 ,且每条边上除顶点外无其它格点.(注:图甲、图乙在答题纸上)
,且每条边上除顶点外无其它格点.(注:图甲、图乙在答题纸上)
相关试题

