【题目】如今,优学派电子书包通过将信息技术与传统教学深度结合,让智能科技在现代教育中发挥了重要作用。某优学派公司筹集资金12.8万元,一次性购进两种新型电子书包访问智能终端:平板电脑和PC机共30台.根据市场需要,这些平板电脑、PC机可以全部销售,全部销售后利润不少于1.5万元,其中平板电脑、PC机的进价和售价见如下表格:

设该公司计划购进平板电脑x台,平板电脑和PC机全部销售后该公司获得的利润为y元.
(1) 试写出y与x的函数关系式;
(2) 该公司有哪几种进货方案可供选择?请写出具体方案;
(3) 选择哪种进货方案,该公司获利最大?最大利润是多少元?
参考答案:
【答案】(1)y= 300x+12000;(2)见解析;(3)购进平板电脑12台,PC机18台。能获得最大利润是15600元.
【解析】试题分析:(1)设该公司计划购进平板电脑x台,则购进PC机(30-x)台,根据题意可得等量关系:公司获得的利润y=平板电脑x台的利润+PC机(30-x)台的利润,根据等量关系可得函数关系式;
(2)根据资金12.8万元和利润不少于1.5万元列出不等式组,解不等式组即可;
(3) 根据一次函数的性质:k>0时,y随x的增大而增大可得答案.
试题解析:
(1)设该公司计划购进平板电脑x台,则购进PC机(30-x)台,
根据题意得:y=(6100﹣5400)x+(3900﹣3500)(30﹣x) ,整理得:y= 300x+12000;
(2)由题意得: ![]() , 解之得:
, 解之得: ![]() ,
,
∴整数x=10,11,或12 ;
所以该公司共有3种进货方案可供选择:
方案一:购进平板电脑10台,PC机20台;
方案二:购进平板电脑11台,PC机19台;
方案三:购进平板电脑12台,PC机18台;
(3)∵对于函数y= 300x+12000,y随x的增大而增大,
∴该公司选择方案三:购进平板电脑12台,PC机18台。能获得最大利润,
此时,最大利润y= 300×12+12000=15600 (元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+kx+81是完全平方式,则k的值应是
-
科目: 来源: 题型:
查看答案和解析>>【题目】列分式方程的步骤:(1)审清题意,明确题目中的未知数;(2)根据题意找,列出分式方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).
(1) 画出△ABC关于y轴的对称图形△A1B1C1;
(2) 画出将△ABC绕原点O按顺时钟旋转180°所得的△A2B2C2;
(3) 在x轴上求作一点P,使△PAB的周长最小,并直接写出点P的坐标.(不写解答过程,直接写出结果)

-
科目: 来源: 题型:
查看答案和解析>>【题目】20190的值等于( )
A.-2019B.0C.1D.2019
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个同学分别解一道一元二次方程x2+bx+c=0,甲因把一次项系数看错了,而解得方程两根为-3和5,乙把常数项看错了,解得两根为2和2,则原方程是 .
-
科目: 来源: 题型:
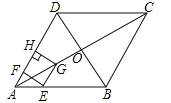
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒
(1)求线段EF的长(用含t的代数式表示);
(2)求点H与点D重合时t的值;
(3)设矩形EFHG与菱形ABCD重叠部分图形的面积与S平方单位,求S与t之间的函数关系式;
(4)矩形EFHG的对角线EH与FG相交于点O′,当OO′∥AD时,t的值为 ;当OO′⊥AD时,t的值为 .
相关试题

