【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y= ![]() 的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为.
的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为.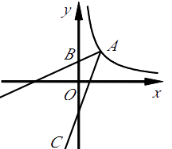
参考答案:
【答案】(-1,-6)
【解析】解:作BF⊥AC于点F,作AE⊥y轴于点E,设AC交y轴于点D,
∵A(2,3),B(0,2)
∴AE=2,BE=1,
∴AB=![]() ,
,
又∵∠BAC=45°,
∴BF=AF=![]() ,
,
∴△DEA∽△DFB,令AD=x,
∴ ![]() =
=![]() ,
,
∴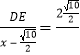
∴DE=![]()
又∵![]()
解得![]() =2
=2![]() ,
,![]() =
=![]() (舍去)
(舍去)
∴AD=2![]() ,
,
设D(0,y)
∴![]() +4=
+4=![]()
解得:![]() =-3,
=-3,![]() =9(舍去)
=9(舍去)
∴设AC直线方程为y=kx+b,将A(2,3),D(0,-3)代入直线方程得,![]() ;解得
;解得![]()
∴AC:y=3x-3,
∵A(2,3)在y=![]() 上,
上,
∴k=2×3=6,
∴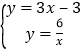 ;解得
;解得![]() ;
;
∴C(-1,-6).
【考点精析】掌握确定一次函数的表达式和勾股定理的概念是解答本题的根本,需要知道确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题6分)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(2,2),B(4,1),C(4,4).

(1)作出 ABC关于原点O成中心对称的
ABC关于原点O成中心对称的  A1B1C1.
A1B1C1.
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在 A1B1C1的内部(不包括顶点和边界),求a的取值范围.
A1B1C1的内部(不包括顶点和边界),求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由.
-
科目: 来源: 题型:
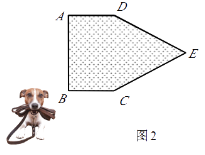
查看答案和解析>>【题目】在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m.拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).
①如图1,若BC=4m,则S=m.
②如图2,现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其它条件不变.则在BC的变化过程中,当S取得最小值时,边BC的长为m.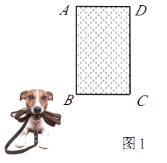
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励市民节约用水,自来水公司特制定了新的用水收费标准,每月用水量,x(吨)与应付水费(元)的函数关系如图.
(1)求出当月用水量不超过5吨时,y与x之间的函数关系式;
(2)某居民某月用水量为8吨,求应付的水费是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了监控一不规则多边形艺术走廊内的活动情况,现已在A,B两处各安装了一个监控探头(走廊内所用探头的观测区域为圆心角最大可取到180°的扇形),图中的阴影部分是A处监控探头观测到的区域.要使整个艺术走廊都能被监控到,还需再安装一个监控探头,则安装的位置是( )

A.E处
B.F处
C.G处
D.H处 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6cm,求CM和AD的长.

相关试题

