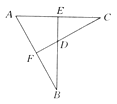
【题目】如图,BE⊥AC于E,CF⊥AB于F,AE=AF,BE与CF交于点D,则:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.以上结论正确的是( )
A. ① B. ② C. ①② D. ①②③
参考答案:
【答案】D
【解析】
∵BE⊥AC,CF⊥AB,
∴∠BEA=∠CFA=90°,
在△ABE与△ACF中,
∵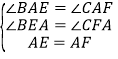 ,
,
∴△ABE≌△ACF(AAS) ①正确,
∴∠B=∠C,AB=AC(全等三角形对应角和对应边相等),
∴BF=CE,
在△BDF与△CDE中,
∵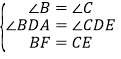 ,
,
∴△BDF≌△CDE(AAS)②正确,
∴DF=DE(全等三角形对应边相等),
∴点D在∠BAC的平分线上(到角的两边距离相等的点,在这个角的平分线上)③正确;
故①②③都正确.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知射线 OC 在∠AOB 的内部,射线 OE 平分∠AOC,射线 OF 平分∠COB.
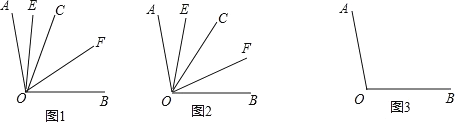
(1)如图 1,若∠AOB=100°,∠AOC=32°,则∠EOF= 度;
(2)若∠AOB=α,∠AOC=β.
①如图 2,若射线 OC 在∠AOB 的内部绕点 O 旋转,求∠EOF 的度数;
②若射线 OC 在∠AOB 的外部绕点 O 旋转(旋转中∠AOC、∠BOC 均是指小于 180°的角),其余条件不变,请借助图 3 探究∠EOF 的大小,直接写出∠EOF 的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(π﹣
 )0+|
)0+| 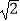 ﹣1|+(
﹣1|+(  )﹣1﹣2sin45°.
)﹣1﹣2sin45°. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某景区的环形游览路线ABCDA,已知从景点C到出口A的两条道路CBA和CDA均为1600米,现有1号、2号两游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形道路连续循环行驶,供游客随时免费乘车(上、下车的时间忽略不计),两车的速度均为200米/分,每一个游客的步行速度均为50米/分.

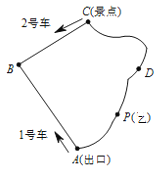

(1)探究(填空):
①当两车行驶 分钟时,1、2号车第一次相遇,此相遇点到出口A的路程为 米;
②当1号车第二次恰好经过点C,此时两车行驶了 分钟,这一段时间内1号车与2号车相遇了 次.
(2)发现:
若游客甲在BC上K处(不与点C、B重合)候车,准备乘车到出口A,在下面两种情况下,请问哪种情况用时较少(含候车时间)?请说明理由.
情况一:若他刚好错过2号车,便搭乘即将到来的1号车;
情况二:若他刚好错过1号车,便搭乘即将到来的2号车.
(3)决策:
①若游客乙在DA上从D向出口A走去,游客乙从D出发时恰好2号车在C处,当步行到DA上一点P(不与A,D重合)时,刚好与2号车相遇,经计算他发现:此时原地(P点)等候乘1号车到出口与直接从P步行到达出口A这两种方式,所花时间相等,请求出D点到出口A的路程.
②当游客丙逛完景点C后准备到出口A,此时2号车刚好在B点,已知BC路程为600米,请你帮助游客丙做一下决策,怎样到出口A所花时间最少,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,5AO=3CO.
(1)写出数轴上点A、C表示的数;
(2)点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒6个单位长度的速度沿数轴向左匀速运动,M为线段AP的中点,点N在线段CQ上,且CN=
 CQ.设运动的时间为t(t>0)秒.
CQ.设运动的时间为t(t>0)秒.①数轴上点M、N表示的数分别是 (用含t的式子表示);
②t为何值时,M、N两点到原点的距离相等?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取利了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:
根据所给信息,解答下列问题: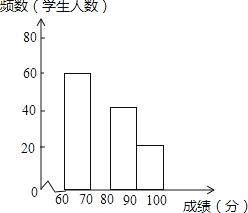
(1)在表中的频数分布表中,m= , n= .成绩
频数
频率
60≤x<70
60
0.30
70≤x<80
m
0.40
80≤x<90
40
n
90≤x≤100
20
0.10
(2)请补全图中的频数分布直方图.
(3)按规定,成绩在80分以上(包括80分)的选手进入决赛.若娄底市共有4000人参数,请估计约有多少人进入决赛?
相关试题

