搜索
【题目】计算：（π﹣ 
）0+| 
﹣1|+（ 
）﹣1﹣2sin45°．
参考答案：
【答案】解：（π﹣ 
）0+| 
﹣1|+（ 
）﹣1﹣2sin45°
=1+ ﹣1+2﹣
=2．
【解析】直接利用特殊角的三角函数值以及绝对值、零指数幂的性质分析得出答案．此题主要考查了实数运算，正确化简各数是解题关键．
【考点精析】通过灵活运用零指数幂法则和整数指数幂的运算性质，掌握零次幂和负整数指数幂的意义： a0=1（a≠0）;a-p=1/ap（a≠0，p为正整数）；aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)即可以解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一个底面直径为 5cm，高为 18cm 的圆柱形瓶内装满水，再将瓶内得水倒入一个底面直径为 6cm，高为 10cm 的圆柱形玻璃杯中，能否完全装下? 若装不下，那么瓶内水面还有多高? 若未能装满，求杯内水面离杯口的距离.
-
科目： 来源： 题型：
查看答案和解析>>【题目】当a、b满足条件a＞b＞0时，
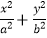=1表示焦点在x轴上的椭圆．若 
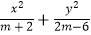=1表示焦点在x轴上的椭圆，则m的取值范围是 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知射线 OC 在∠AOB 的内部，射线 OE 平分∠AOC，射线 OF 平分∠COB．
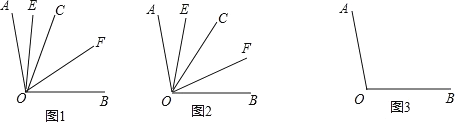
（1）如图 1，若∠AOB=100°，∠AOC=32°，则∠EOF= 度；
（2）若∠AOB=α，∠AOC=β．
①如图 2，若射线 OC 在∠AOB 的内部绕点 O 旋转，求∠EOF 的度数；
②若射线 OC 在∠AOB 的外部绕点 O 旋转(旋转中∠AOC、∠BOC 均是指小于 180°的角)，其余条件不变，请借助图 3 探究∠EOF 的大小，直接写出∠EOF 的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是某景区的环形游览路线ABCDA，已知从景点C到出口A的两条道路CBA和CDA均为1600米，现有1号、2号两游览车分别从出口A和景点C同时出发，1号车顺时针、2号车逆时针沿环形道路连续循环行驶，供游客随时免费乘车（上、下车的时间忽略不计），两车的速度均为200米/分，每一个游客的步行速度均为50米/分．
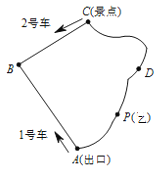
（1）探究（填空）：
①当两车行驶 分钟时，1、2号车第一次相遇，此相遇点到出口A的路程为 米；
②当1号车第二次恰好经过点C，此时两车行驶了 分钟，这一段时间内1号车与2号车相遇了 次．
（2）发现：
若游客甲在BC上K处（不与点C、B重合）候车，准备乘车到出口A，在下面两种情况下，请问哪种情况用时较少（含候车时间）？请说明理由．
情况一：若他刚好错过2号车，便搭乘即将到来的1号车；
情况二：若他刚好错过1号车，便搭乘即将到来的2号车．
（3）决策：
①若游客乙在DA上从D向出口A走去，游客乙从D出发时恰好2号车在C处，当步行到DA上一点P（不与A，D重合）时，刚好与2号车相遇，经计算他发现：此时原地（P点）等候乘1号车到出口与直接从P步行到达出口A这两种方式，所花时间相等，请求出D点到出口A的路程．
②当游客丙逛完景点C后准备到出口A，此时2号车刚好在B点，已知BC路程为600米，请你帮助游客丙做一下决策，怎样到出口A所花时间最少，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，BE⊥AC于E，CF⊥AB于F，AE=AF，BE与CF交于点D，则：①△ABE≌△ACF；②△BDF≌△CDE；③点D在∠BAC的平分线上．以上结论正确的是( )
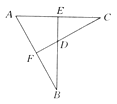
A. ① B. ② C. ①② D. ①②③
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，O为直线AB上一点，∠AOC＝50°，OD平分∠AOC，∠DOE＝90°.
(1)请你数一数，图中有多少个小于平角的角；
(2)求出∠BOD的度数；
(3)请通过计算说明OE是否平分∠BOC.
相关试题
