搜索
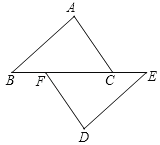
【题目】如图，点B、F、C、E在同一条直线上，点A、D在直线BC的异侧，AB=DE，AC=DF，BF=EC．
（1）求证：△ABC≌△DEF；
（2）若∠BFD=150°，求∠ACB的度数．
参考答案：
【答案】（1）见解析；（2）30°
【解析】
（1）根据BF=EC，可以得到BC=EF，然后根据题目中的条件，利用全等三角形的判定即可证明结论成立；
（2）根据邻补角互补和全等三角形的性质可以得到∠ACB的度数．
（1）∵BF=EC，∴BF+FC=EC+FC，∴BC=EF．
在△ABC和△DEF中，∵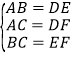
，∴△ABC≌△DEF（SSS）；
（2）∵∠BFD=150°，∠BFD+∠DFE=180°，∴∠DFE=30°．
由（1）知：△ABC≌△DEF，∴∠ACB=∠DFE，∴∠ACB=30°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将四根长度相等的细木条首尾相接，用钉子钉成四边形ABCD，转动这个四边形，使它形状改变，当∠C=90°时，测得AC=2
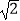，当∠C=120°时，如图2，AC=（ ）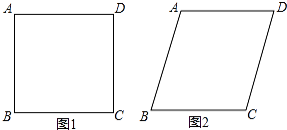 
A.2
B.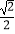
C.
D. -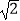
科目： 来源： 题型：
查看答案和解析>>【题目】如图，⊙O的半径为2，AB，CD是互相垂直的两条直径，点P是⊙O上任意一点（P与A，B，C，D不重合），过点P作PM⊥AB于点M，PN⊥CD于点N，点Q是MN的中点，当点P沿着圆周转过45°时，线段OQ所扫过过的面积为（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
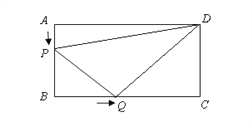
查看答案和解析>>【题目】如图所示，在长方形ABCD中，AB＝6厘米,BC＝12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动，点Q沿BC从点B开始向点C以2厘米/秒的速度移动，如果P、Q同时出发，用t(秒)表示移动的时间（0≤t≤6）．
（1）当PB＝2厘米时，求点P移动多少秒？
（2）t为何值时，△PBQ为等腰直角三角形？
（3）求四边形PBQD的面积，并探究一个与计算结果有关的结论．
-
科目： 来源： 题型：
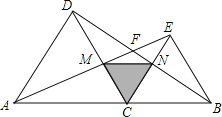
查看答案和解析>>【题目】如图，点C是线段AB上除A、B外的任意一点，分别以AC、BC为边在线段AB的同旁作等边三角形ACD和等边三角形BEC，连结AE交DC于M，连结BD交CE于N，AE与BD交于F
（1）求证：AE=BD；
（2）连结MN，仔细观察△MNC的形状，猜想△MNC是什么三角形？说出你的猜想，并加以证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC是等边三角形，点D、E分别在AC、BC上，且CD=BE，
（1）求证：△ABE≌△BCD；
（2）求出∠AFB的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠ABC=90°，AB=2，BC=4，现将△ABC绕顶点B顺时针方向旋转△A′BC′的位置，此时A′C′与BC的交点D是BC的中点，则线段C′D的长度是（ ）
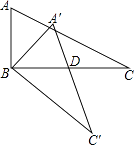
A.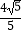
B.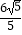
C.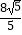
D.2
相关试题
