搜索
【题目】（1）如果
=0，求[（x2＋y2）＋2y（x－y）－（x－y）（x+3y）]÷4y的值.
（2）先化简，再求值：(2＋a)(2－a)＋a(a－5b)＋3a5b3÷(－a2b)2，其中ab＝－
.
参考答案：
【答案】（1）原式= 
，把y=-2代入得 原式=﹣1；（2）4－2ab ，5
【解析】试题分析：(1)据非负数性质得到
， 
，解得
,然后利用整式的混合运算求值.(2) 原式第一项利用平方差公式化简，第二项利用单项式乘以多项式法则计算，最后一项先计算乘方运算，再计算除法运算，合并得到最简结果，把ab的值代入计算即可求出值．
本题解析:(1)由题意得： 
， 
,则
所以[（x2＋y2）＋2y（x－y）－（x－y）（x+3y）]÷4y=
= 
=
(2) 原式=
,当ab=12时，原式=4+1=5.
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列各式中，合并同类项正确的是（ ）
A. 2x+x=2x2 B. 2x+x=3x C. a2+a2=a4 D. 2x+3y=5xy
-
科目： 来源： 题型：
查看答案和解析>>【题目】在半径为R的圆形钢板上，挖去四个半径都为r的小圆.若R＝16.8，剩余部分的面积为272π，则r的值是（ ）
A. 3.2 B. 2.4 C. 1.6 D. 0.8
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线
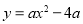（a＞0）与x轴相交于A，B两点（点A在点B的左侧），点P是抛物线上一点，且PB=AB，∠PBA=120°，如图所示．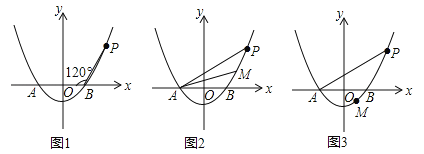
（1）求抛物线的解析式．
（2）设点M（m，n）为抛物线上的一个动点，且在曲线PA上移动．
①当点M在曲线PB之间（含端点）移动时，是否存在点M使△APM的面积为
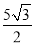？若存在，求点M的坐标；若不存在，请说明理由．②当点M在曲线BA之间（含端点）移动时，求|m|+|n|的最大值及取得最大值时点M的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一元二次方程（x﹣4）2=2x﹣3化为一般式是（ ）
A. x2﹣10x+13=0 B. x2﹣10x+19=0 C. x2﹣6x+13=0 D. x2﹣6x+19=0
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图为放置在水平桌面上的台灯的平面示意图，灯臂AO长为40cm，与水平面所形成的夹角∠OAM为75°．由光源O射出的边缘光线OC，OB与水平面所形成的夹角∠OCA，∠OBA分别为90°和30°，求该台灯照亮水平面的宽度BC（不考虑其他因素，结果精确到0.1cm．温馨提示：sin75°≈0.97，cos75°≈0.26，
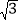≈1.73）．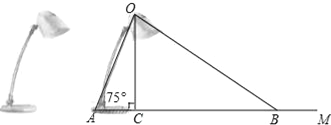
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果关于x的一元二次方程ax2＋bx＋c＝0有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”。
（1）请问一元二次方程x2－3x＋2＝0是倍根方程吗？如果是，请说明理由。
（2）若一元二次方程ax2＋bx－6＝0是倍根方程，且方程有一个根为2，求a、b的值？
相关试题
