搜索
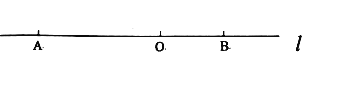
【题目】如图，直线
上有
两点，
， 点
是线段
上的一点，
.若动点
，
分别从同时出发，向右运动，点的速度为
.点的速度为
.设运动时间为
，当点和点重合时，
两点停止运动.
（1）当
为何值时，
？
（2）当点经过点时，动点
从点出发，以
的速度也向右运动，当点追上点后立即返回，以的速度向点运动，遇到点后再立即返回，以的速度向点运动，如此往返，当点与点重合时，两点停止运动，此时点也停止运动，在此过程中，点行驶的总路程是多少？
参考答案：
【答案】（1）2s或6.8s（2）20cm
【解析】
（1）先由OA=2OB结合AB=OA+OB=18即可求出OA、OB的长度；分两种情况,由两点间的距离公式结合2OP-OQ=4即可得出关于t的一元一次方程，解之即可得出结论；
（2）点M运动的时间就是点P从点O开始到追到点Q的时间，用这个时间乘以速度即可．
解：（1）∵AB=18cm，OA=2OB，
∴OA+OB=3OB=AB=18cm，
解得：OB=6cm，
OA=2OB=12cm．
12÷3=4秒，当0<t≤4时，如图，
AP=3t，OP=12-3t，BQ=t，OQ=6+t，
∵2OP-OQ=4，
∴2(12-3t)-(6+t)=4，
解得
t=2；
当点P与点Q重合时，
3t=18+t，
t=9，
当4＜t≤9时，如图，
OP=3t-12，OQ=6+t，
则2(3t-12)-(6+t)=4，
解得t=6.8．
故当t为2s或6.8s时，2OP-OQ=4；
（2）4×（9-4）=20（cm）．
答：在此过程中，点M行驶的总路程是20cm．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有A、B两组卡片共5张，A组的三张分别写有数字2，4，6，B组的两张分别写有3，5．它们除了数字外没有任何区别，
（1）随机从A组抽取一张，求抽到数字为2的概率；
（2）随机地分别从A组、B组各抽取一张，请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则：若选出的两数之积为3的倍数，则甲获胜；否则乙获胜．请问这样的游戏规则对甲乙双方公平吗？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市中小学全面开展“阳光体育”活动，某校在大课间中开设了A：体操，B：跑操，C：舞蹈，D：健美操四项活动，为了解学生最喜欢哪一项活动，随机抽取了部分学生进行调查，并将调查结果绘制成了如下两幅不完整的统计图，请根据统计图回答下列问题：
（1）这次被调查的学生共有 人．
（2）请将统计图2补充完整．
（3）统计图1中B项目对应的扇形的圆心角是 度．
（4）已知该校共有学生3600人，请根据调查结果估计该校喜欢健美操的学生人数．
-
科目： 来源： 题型：
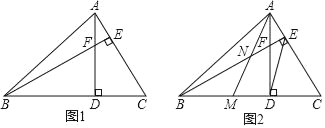
查看答案和解析>>【题目】如图1，在锐角△ABC中，∠ABC=45°，高线AD、BE相交于点F．
（1）判断BF与AC的数量关系并说明理由；
（2）如图2，将△ACD沿线段AD对折，点C落在BD上的点M，AM与BE相交于点N，当DE∥AM时，判断NE与AC的数量关系并说明理由．
【答案】（1）BF=AC，理由见解析；（2）NE=
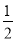AC，理由见解析.【解析】试题分析：（1）如图1，证明△ADC≌△BDF（AAS），可得BF=AC；
（2）如图2，由折叠得：MD=DC，先根据三角形中位线的推论可得：AE=EC，由线段垂直平分线的性质得：AB=BC，则∠ABE=∠CBE，结合（1）得：△BDF≌△ADM，则∠DBF=∠MAD，最后证明∠ANE=∠NAE=45°，得AE=EN，所以EN=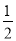
AC．试题解析：
（1）BF=AC，理由是：
如图1，∵AD⊥BC，BE⊥AC，
∴∠ADB=∠AEF=90°，
∵∠ABC=45°，
∴△ABD是等腰直角三角形，
∴AD=BD，
∵∠AFE=∠BFD，
∴∠DAC=∠EBC，
在△ADC和△BDF中，
∵
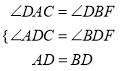，∴△ADC≌△BDF（AAS），
∴BF=AC；
（2）NE=
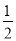AC，理由是：如图2，由折叠得：MD=DC，
∵DE∥AM，
∴AE=EC，
∵BE⊥AC，
∴AB=BC，
∴∠ABE=∠CBE，
由（1）得：△ADC≌△BDF，
∵△ADC≌△ADM，
∴△BDF≌△ADM，
∴∠DBF=∠MAD，
∵∠DBA=∠BAD=45°，
∴∠DBA﹣∠DBF=∠BAD﹣∠MAD，
即∠ABE=∠BAN，
∵∠ANE=∠ABE+∠BAN=2∠ABE，
∠NAE=2∠NAD=2∠CBE，
∴∠ANE=∠NAE=45°，
∴AE=EN，
∴EN=
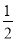AC．【题型】解答题
【结束】
19【题目】某校学生会决定从三明学生会干事中选拔一名干事当学生会主席，对甲、乙、丙三名候选人进行了笔试和面试，三人的测试成绩如下表所示：
测试项目
测试成绩/分
甲
乙
丙
笔试
75
80
90
面试
93
70
68
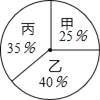
根据录用程序，学校组织200名学生采用投票推荐的方式，对三人进行民主测评，三人得票率如扇形统计图所示（没有弃权，每位同学只能推荐1人），每得1票记1分．
（1）分别计算三人民主评议的得分；
（2）根据实际需要，学校将笔试、面试、民主评议三项得分按3：3：4的比例确定个人成绩，三人中谁会当选学生会主席？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点．请你观察图中正方形A1B1C1D1，A2B2C2D2，A3B3C3D3…每个正方形四条边上的整点的个数．按此规律推算出正方形A10B10C10D10四条边上的整点共有______个．
-
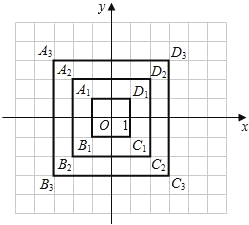
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，平行四边形ABCD的顶点A，B的坐标分别为（-2，0），（
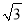，0），AD=2，∠DAB=60°点P从点A出发沿A→D→C运动到点C，连接PO．当PO=OB时，点P的坐标为___.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场准备进一批两种不同型号的衣服，已知购进A种型号衣服9件，B种型号衣服10件，则共需1810元；若购进A种型号衣服12件，B种型号衣服8件，共需1880元；已知销售一件A型号衣服可获利18元，销售一件B型号衣服可获利30元，要使在这次销售中获利不少于699元，且A型号衣服不多于28件．
（1）求A、B型号衣服进价各是多少元？
（2）若已知购进A型号衣服是B型号衣服的2倍还多4件，则商店在这次进货中可有几种方案并简述购货方案．
相关试题
