【题目】如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为( )
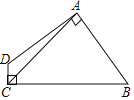
A. 15 B. 12.5 C. 14.5 D. 17
参考答案:
【答案】B
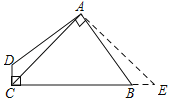
【解析】过A作AE⊥AC,交CB的延长线于E,判定△ACD≌△AEB,即可得到△ACE是等腰直角三角形,四边形ABCD的面积与△ACE的面积相等,根据S△ACE=![]() ×5×5=12.5,即可得出结论.
×5×5=12.5,即可得出结论.
如图,过A作AE⊥AC,交CB的延长线于E,
∵∠DAB=∠DCB=90°,
∴∠D+∠ABC=180°=∠ABE+∠ABC,
∴∠D=∠ABE,
又∵∠DAB=∠CAE=90°,
∴∠CAD=∠EAB,
又∵AD=AB,
∴△ACD≌△AEB,
∴AC=AE,即△ACE是等腰直角三角形,
∴四边形ABCD的面积与△ACE的面积相等,
∵S△ACE=![]() ×5×5=12.5,
×5×5=12.5,
∴四边形ABCD的面积为12.5,
故选B.
-
科目: 来源: 题型:
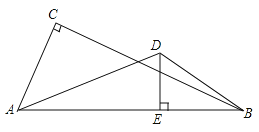
查看答案和解析>>【题目】如图,学校位于高速路AB的一侧(AB成一条直线),点A,B为高速路上距学校直线距离最近的2个隧道出入口,点C、D为学校的两栋教学楼,经测量∠ACB=90°,∠ADB>90°,AC=600m,AB=1000m,点D到高速路的最短直线距离DE=400m.
(1)求教学楼C到隧道口B的直线距离;
(2)比较AC2+BC2与AD2+BD2谁大谁小,试用计算说明.
-
科目: 来源: 题型:
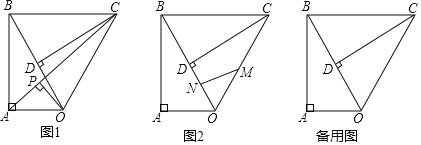
查看答案和解析>>【题目】已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O顺时针旋转60°,如题图1,连接BC.
(1)填空:∠OBC= °;
(2)如图1,连接AC,作OP⊥AC,垂足为P,求OP的长度;
(3)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒,设运动时间为x秒,△OMN的面积为y,求当x为何值时y取得最大值?最大值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为线段
为线段 上一动点,分别过点
上一动点,分别过点 作
作 ,
, ,连接
,连接 .已知
.已知 ,设
,设 .
.(1)用含
 的代数式表示
的代数式表示 的值;
的值;(2)探究:当点
 满足什么条件时,
满足什么条件时, 的值最小?最小值是多少?
的值最小?最小值是多少?(3)根据(2)中的结论,请构造图形求代数式
 的最小值.
的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB、AC于点D、E,则以下AE与CE的数量关系正确的是( )

A.AE=
 CEB.AE=
CEB.AE=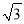 CEC.AE=
CEC.AE=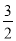 CED.AE=2CE
CED.AE=2CE -
科目: 来源: 题型:
查看答案和解析>>【题目】在学习完《有理数》后,小奇对运算产生了浓厚的兴趣.借助有理数的运算,定义了一种新运算“⊕”,规则如下:a⊕b=a×b+2×a.
(1)求2⊕(﹣1)的值;
(2)求﹣3⊕(﹣4⊕
 )的值;
)的值;(3)试用学习有理数的经验和方法来探究这种新运算“⊕”是否具有交换律?请写出你的探究过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着手机的普及,微信(一种聊天软件)的兴起,许多人抓住这种机会,做起了“微商”很多农产品也改变了原来的销售模式,实行了网上销售,刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖
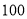 斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况(超额记为正,不足记为负单位:斤);
斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况(超额记为正,不足记为负单位:斤);星期
一
二
三
四
五
六
日
与计划量的差值
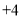
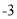
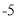
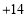
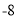
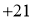
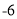
(1)根据记录的数据可知前三天共卖出 斤;
(2)根据记录的数据可知该周销售量最多的一天比销售量最少的一天多销售 斤;
(3)本周实际销售总量是否达到了计划数量?试通过计算说明理由.
(4)若冬枣每斤按
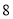 元出售,每斤冬枣的运费平均
元出售,每斤冬枣的运费平均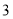 元(运费由小明承担),那么小明本周一共收入多少元?
元(运费由小明承担),那么小明本周一共收入多少元?
相关试题

