Question

【题目】如图，梯形中，AB∥DC，AB⊥BC，AB＝2cm，CD＝4cm．以BC上一点O为圆心的圆经过A、D两点，且，圆心O到弦AD的距离是____cm.

Answer 1

【答案】.

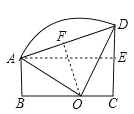
【解析】试题分析：如图，作AE⊥CD，垂足为E，OF⊥AD，垂足为F，

则四边形AECB是矩形，

CE=AB=2cm，DE=CD﹣CE=4﹣2=2cm，

∵∠AOD=90°，AO=OD，

所以△AOD是等腰直角三角形，

AO=OD，∠OAD=∠ADO=45°，BO=CD，

∵AB∥CD，

∴∠BAD+∠ADC=180°

∴∠ODC+∠OAB=90°，

∵∠ODC+∠DOC=90°，

∴∠DOC=∠BAO，

∵∠B=∠C=90°

∴△ABO≌△OCD，

∴OC=AB=2cm，OB=CD=4cm，BC=BO+OC=AE=6cm，

由勾股定理知，AD2=AE2+DE2，

得AD=2cm，

∴AO=OD=2cm，

S△AOD=AODO=ADOF，

∴OF=cm．